Эллипсе – Эллипс. Формулы, признаки и свойства эллипсa

Эллипс. Формулы, признаки и свойства эллипсa

F₁ и F₂ — фокусы эллипсa

Оси эллипсa.

А₁А₂ = 2a — большая ось эллипса (проходит через фокусы эллипса)

B₁B₂ = 2b — малая ось эллипса (перпендикулярна большей оси эллипса и проходит через ее центр)

a — большая полуось эллипса

b — малая полуось эллипса

O — центр эллипса (точка пересечения большей и малой осей эллипса)

Вершины эллипсa A₁, A₂, B₁, B₂ — точки пересечения эллипсa с малой и большой осями эллипсa

Диаметр эллипсa — отрезок, соединяющий две точки эллипса и проходящий через его центр.

Фокальное расстояние c — половина длины отрезка, соединяющего фокусы эллипсa.

Эксцентриситет эллипсa e характеризует его растяженность и определяется отношением фокального расстояния c к большой полуоси a. Для эллипсa эксцентриситет всегда будет 0 e e = 0, для параболы e = 1, для гиперболы e > 1.

Фокальные радиусы эллипсa r₁, r₂ — расстояния от точки на эллипсе до фокусов.

Радиус эллипсa R — отрезок, соединяющий центр эллипсa О с точкой на эллипсе.

R =	ab	=	b
	√a2sin2φ + b2cos2φ		√1 — e2cos2φ

где e — эксцентриситет эллипсa, φ — угол между радиусом и большой осью A₁A₂. Фокальный параметр эллипсa p — отрезок который выходит из фокуса эллипсa и перпендикулярный большой полуоси: Коэффициент сжатия эллипсa (эллиптичность) k — отношение длины малой полуоси к большой полуоси. Так как малая полуось эллипсa всегда меньше большей, то k k = 1:

k = √1 — e²

где e — эксцентриситет. Сжатие эллипсa (1 — k ) — величина, которая равная разности между единицей и эллиптичностью:

Директрисы эллипсa — две прямые перпендикулярные фокальной оси эллипса, и пересекающие ее на расстоянии ae от центра эллипса. Расстояние от фокуса до директрисы равно pe.

ru.onlinemschool.com

Эллипс — это… Что такое Эллипс?

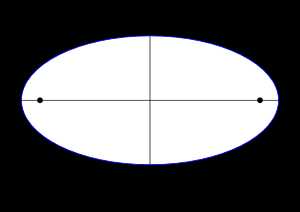Эллипс, его фокусы и главные оси 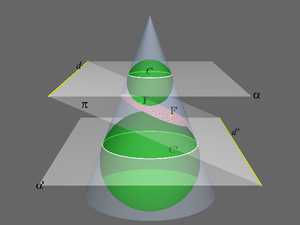Эллипс как коническое сечение, его фокусы и директрисы, получаемые геометрически с помощью шаров Данделена.

Э́ллипс (др.-греч. ἔλλειψις — опущение, недостаток, в смысле недостатка эксцентриситета до 1) — геометрическое место точек M Евклидовой плоскости, для которых сумма расстояний до двух данных точек и (называемых фокусами) постоянна и больше расстояния между фокусами, то есть

причем

Окружность является частным случаем эллипса. Наряду с гиперболой и параболой, эллипс является коническим сечением и квадрикой.

Эллипс также можно описать как пересечение плоскости и кругового цилиндра или как ортогональную проекцию окружности на плоскость.

Связанные определения

• Проходящий через фокусы эллипса отрезок AB, концы которого лежат на эллипсе, называется большой осью данного эллипса. Длина большой оси равна 2a в вышеприведённом уравнении.
• Отрезок CD, перпендикулярный большой оси эллипса, проходящий через центральную точку большой оси, концы которого лежат на эллипсе, называется малой осью эллипса.
• Отрезки, проведённые из центра эллипса к вершинам на большой и малой осях называются, соответственно, большой полуосью и малой полуосью эллипса, и обозначаются a и b.
• Точка пересечения большой и малой осей эллипса называется его центром.
• Расстояния и от каждого из фокусов до данной точки на эллипсе называются фокальными радиусами в этой точке.
• Расстояние называется фокальным расстоянием.
• Величина называется эксцентриситетом.
• Диаметром эллипса называют произвольную хорду, проходящую через его центр. Сопряжёнными диаметрами эллипса называют пару его диаметров, обладающих следующим свойством: середины хорд, параллельных первому диаметру, лежат на втором диаметре. В этом случае и середины хорд, параллельных второму диаметру, лежат на первом диаметре.
• Радиус эллипса в данной точке (расстояние от его центра до данной точки) вычисляется по формуле , где  — угол между радиус-вектором данной точки и осью абсцисс.
• Фокальным параметром называется половина длины хорды, проходящей через фокус и перпендикулярной большой оси эллипса.
• Отношение длин малой и большой полуосей называется коэффициентом сжатия эллипса или эллиптичностью: Величина, равная называется сжатием эллипса. Для окружности коэффициент сжатия равен единице, сжатие — нулю. Коэффициент сжатия и эксцентриситет эллипса связаны соотношением
• Для каждого из фокусов существует прямая, называемая директрисой, такая, что отношение расстояния от произвольной точки эллипса до его фокуса к расстоянию от этой точки до данной прямой равно эксцентриситету эллипса. Весь эллипс лежит по ту же сторону от такой прямой, что и фокус. Уравнения директрис эллипса в каноническом виде записываются как для фокусов соответственно. Расстояние между фокусом и директрисой равно

Свойства

• Оптические
  • Свет от источника, находящегося в одном из фокусов, отражается эллипсом так, что отраженные лучи пересекутся во втором фокусе.
  • Свет от источника, находящегося вне любого фокусов, отражается эллипсом так, что отраженные лучи ни в каком фокусе не пересекутся.
• Если и — фокусы эллипса, то для любой точки X, принадлежащей эллипсу, угол между касательной в этой точке и прямой равен углу между этой касательной и прямой .
• Прямая, проведённая через середины отрезков, отсечённых двумя параллельными прямыми, пересекающими эллипс, всегда будет проходить через центр эллипса. Это позволяет построением с помощью циркуля и линейки легко получить центр эллипса, а в дальнейшем оси, вершины и фокусы.
• Эволютой эллипса является астроида.
• Точки пересечения эллипса с осями являются его вершинами.
• Эксцентриситет эллипса равен отношению Эксцентриситет характеризует вытянутость эллипса. Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут.
• Эллипс также можно описать как

Соотношения между элементами эллипса

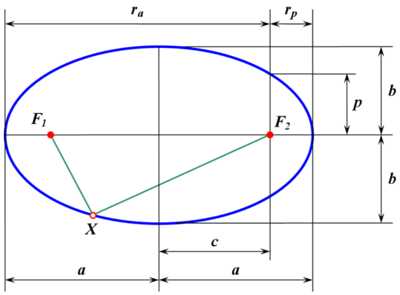Части эллипса (описание см. в разделе «Связанные определения»)

.

Координатное представление

Эллипс как кривая второго порядка

Эллипс является центральной невырожденной кривой второго порядка и удовлетворяет общему уравнению вида

при инвариантах и где:

Соотношения между инвариантами кривой второго порядка и полуосями эллипса:

Каноническое уравнение

Для любого эллипса можно найти декартову систему координат такую, что эллипс будет описываться уравнением (каноническое уравнение эллипса):

Оно описывает эллипс с центром в начале координат, оси которого совпадают с осями координат.

Соотношения  

Уравнения в параметрической форме

Геометрическая иллюстрация параметризации эллипса (анимация).

Каноническое уравнение эллипса может быть параметризовано:

где — параметр уравнения.

В случае окружности параметр является углом между радиус-вектором данной точки и положительным направлением оси абсцисс.

В полярных координатах

Если принять фокус эллипса за полюс, а большую ось — за полярную ось, то его уравнение в полярных координатах будет иметь вид

где e — эксцентриситет, а p — фокальный параметр. При положительном знаке перед e второй фокус эллипса будет находиться в точке а при отрицательном — в точке где фокальное расстояние

Если принять центр эллипса за полюс, а большую ось — за полярную ось, то его уравнение в полярных координатах будет иметь вид

Длина дуги эллипса

Длина дуги плоской линии определяется по формуле:

Воспользовавшись параметрическим представлением эллипса получаем следующее выражение:

После замены выражение для длины дуги принимает окончательный вид:

Получившийся интеграл принадлежит семейству эллиптических интегралов, которые в элементарных функциях не выражаются, и сводится к эллиптическому интегралу второго рода . В частности, периметр эллипса равен:

,

где — полный эллиптический интеграл второго рода.

Приближённые формулы для периметра

Максимальная погрешность этой формулы ~0,63 % при эксцентриситете эллипса ~0,988 (соотношение осей ~1/6,5). Погрешность всегда положительная.

Приблизительно в два раза меньшие погрешности в широком диапазоне эксцентриситетов дает формула:

, где

Максимальная погрешность этой формулы ~0,36 % при эксцентриситете эллипса ~0,980 (соотношение осей ~1/5). Погрешность также всегда положительная.

Cущественно лучшую точность при обеспечивает формула Рамануджана:

При эксцентриситете эллипса ~0,980 (соотношение осей ~1/5) погрешность составляет ~0,02 %. Погрешность всегда отрицательная.

Площадь эллипса и его сегмента

Площадь эллипса вычисляется по формуле

Площадь сегмента между дугой, выпуклой влево, и хордой, проходящей через точки и

^{[источник не указан 156 дней]}

Если эллипс задан уравнением , то площадь можно определить по формуле

.

Построение эллипса

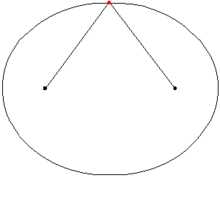Построение с помощью иголок, нитки и карандаша.

Основная статья — статья «Построение эллипса» в Викиучебнике.

Инструментами для рисования эллипса являются:

• эллипсограф;
• две иголки, воткнутые в фокусы эллипса и соединённые ниткой длиной 2a, которую оттягивают карандашом.

При помощи циркуля или циркуля и линейки можно построить любое количество точек, принадлежащих эллипсу, но не весь эллипс целиком.

См. также

Литература

• Корн Г., Корн Т. Свойства окружностей, эллипсов, гипербол и парабол // Справочник по математике. — 4-е издание. — М.: Наука, 1978. — С. 70—73.

Ссылки

dic.academic.ru

Эллипс. Полуоси эллипса. Фокус эллипса.

Эллипс- замкнутая кривая на плоскости, которая может быть получена как пересечение плоскости и кругового цилиндра или как ортогональная проекция окружности на плоскость. На рисунке ниже показано несколько примеров.

 

Круг-это частный случай эллипса, который получается, когда сечение через конус или цилиндр ортогонально оси конуса или цилиндра.

Эллипс-это фигура, в результате сечения конуса и прямого кругового цилиндра

Эллипс симметричен относительно горизонтальной и вертикальной осей, как показано на рисунке выше. Максимальное расстояние между двумя  точками происходит вдоль горизонтальной оси (называемой главной осью или поперечным диаметром), а минимальное расстояние между двумя  точками-вдоль вертикальной оси (называемой малой осью или сопряженным диаметром). Антиподальные точки — это любые две точки по периметру эллипса, так что соединяющий их отрезок линии должен проходить через центр с эллипса (что происходит на пересечении горизонтальной и вертикальной осей). Эллипс симметричен относительно его большой и малой осей.
 

Полуось — это та часть оси, которая лежит между центром \(C\) и периметром эллипса — называется полуосью. Полуоси, принадлежащие к главной оси —  большая полуось, а полуось, принадлежащих к малой оси —  малая полуось. На приведенной выше рисунке мы обозначили каждую из двух полуосей \(a\) и каждую из двух полуосей \(b\). Точки, показанные красным цветом по периметру эллипса, являются точками, где большая и малая оси пересекают периметр эллипса. Это вершины эллипса. Вершины — это точки, в которых кривизна эллипса максимальна (т. е. где главная ось пересекает периметр эллипса). 

 

Есть две специальные точки, которые лежат на главной оси эллипса, равноудаленной от его центра C, каждая из которых является фокусом эллипса. Эти две точки (совместно называемые фокусами эллипса) обычно обозначаются как \(F1\) и \(F2\). Расположение фокусов таково, что для любой точки \(p\) по периметру эллипса сумма расстояний от \(F1\) до \(P\) и от \(F2\) до \(P\) остается постоянной и будет равна длине главной оси. Фактически, принимая любую произвольную пару точек в качестве фокусов и любое значение длины главной оси, которое больше расстояния между этими двумя точками, соответствующий эллипс определяется как набор точек, для которых сумма расстояний между точкой и каждым из фокусов равна длине главной оси.

Сумма расстояний от фокусов до любой точки эллипса есть постоянная
 

Расстояние между любым из фокусов и центром эллипса называется фокусным расстоянием и будет зависеть от длины главной и малой осей. Мы обозначили отрезки линии, соединяющие каждый фокус с центром эллипса \(C\). Длину\( c\) (т. е. Фокусное расстояние) можно найти по следующей формуле:

\(с= \sqrt{a^2-b^2} \)

 

где \(a\) и \(b\)-длины главной и малой осей соответственно. Обратите внимание, что чем дальше фокусы от центра эллипса, тем меньше сходство между эллипсом и окружностью. Кривизна в вершинах эллипса будет увеличиваться, в то время как кривизна в \(cо\)-вершинах будет уменьшаться. Другими словами, эллипс станет более плоским по мере увеличения значения \(c\).

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

myalfaschool.ru

Лекция 15. Эллипс

Лекции по алгебре и геометрии. Семестр 1.

Лекция 15. Эллипс.

Краткое содержание: определение эллипса, основная терминология, каноническая для эллипса система координат и каноническое уравнение эллипса, параметрические уравнения эллипса, эллипс как результат сжатия окружности, касательная к эллипсу, зеркальное свойство эллипса, директрисы и фокальный параметр эллипса, второе определение эллипса.

Глава 15. Эллипс.

п.1. Основные определения.

Определение. Эллипсом называется ГМТ плоскости сумма расстояний которых до двух фиксированных точек плоскости, называемых фокусами, есть величина постоянная.

рис.1.

Определение. Расстояние от произвольной точки М плоскости до фокуса эллипса называется фокальным радиусом точки М.

Обозначения: 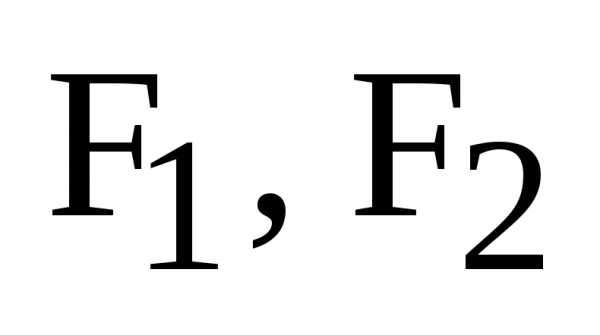– фокусы эллипса, 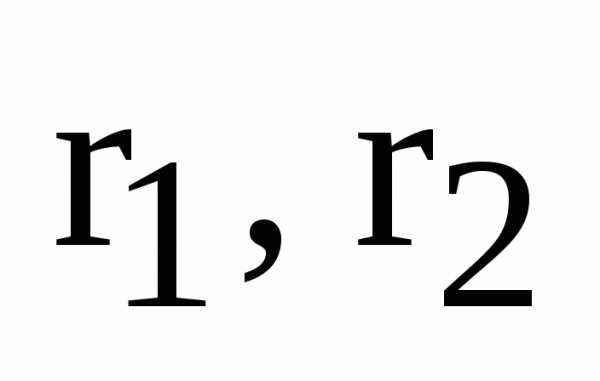– фокальные радиусы точки М.

По определению эллипса, точка М является точкой эллипса тогда и только тогда, когда 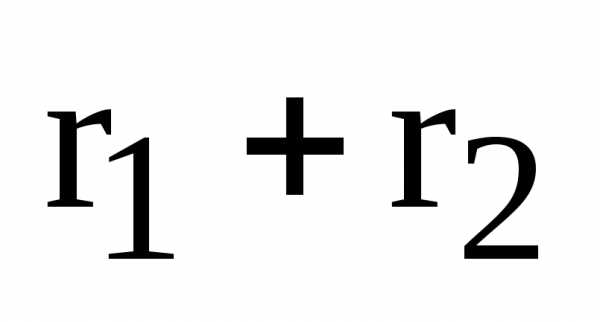– постоянная величина. Эту постоянную принято обозначать 2а:

. (1)

Заметим, что .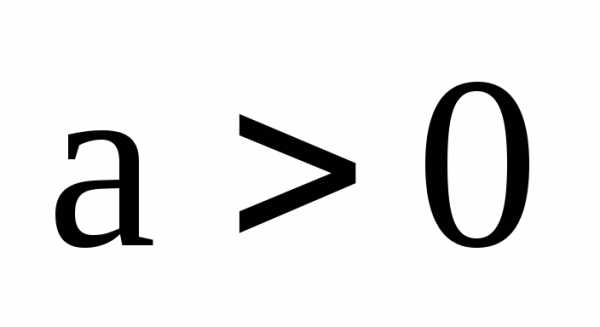

По определению эллипса, его фокусы есть фиксированные точки, поэтому расстояние между ними есть также величина постоянная для данного эллипса.

Определение. Расстояние между фокусами эллипса называется фокусным расстоянием.

Обозначение: .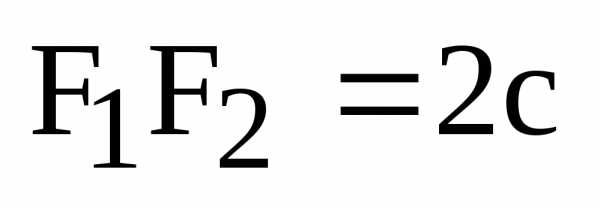

Из треугольника 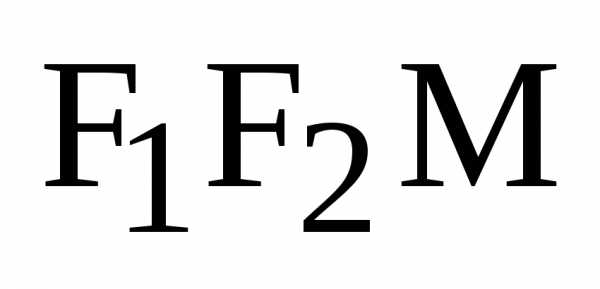следует, что , т.е.

.

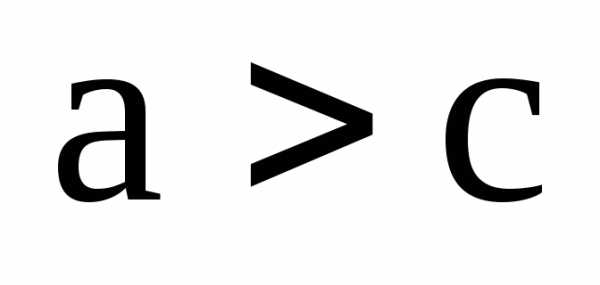Обозначим через b число равное 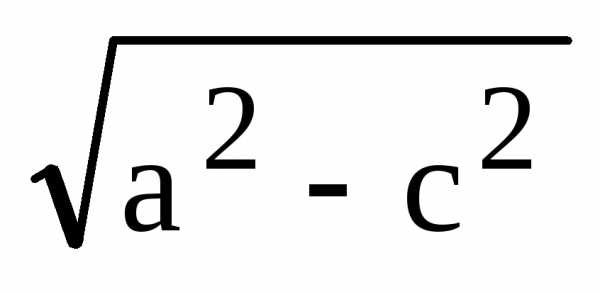, т.е.

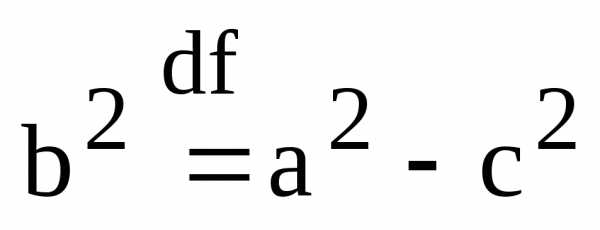. (2)

Определение. Отношение

(3)

называется эксцентриситетом эллипса.

Введем на данной плоскости систему координат, которую мы будем называть канонической для эллипса.

Определение. Ось, на которой лежат фокусы эллипса, называется фокальной осью.

Построим каноническую для эллипса ПДСК, см. рис.2.

В качестве оси абсцисс выбираем фокальную ось, а ось ординат проводим через середину отрезка 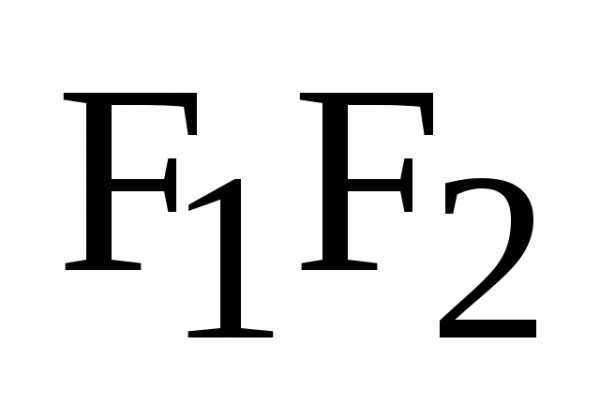перпендикулярно фокальной оси.

рис.2.

Тогда фокусы имеют координаты , .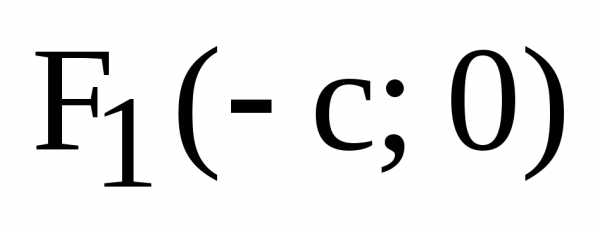

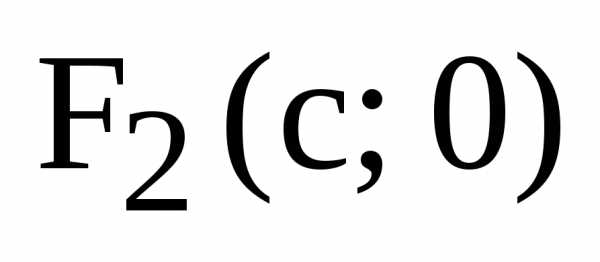п.2. Каноническое уравнение эллипса.

Теорема. В канонической для эллипса системе координат уравнение эллипса имеет вид:

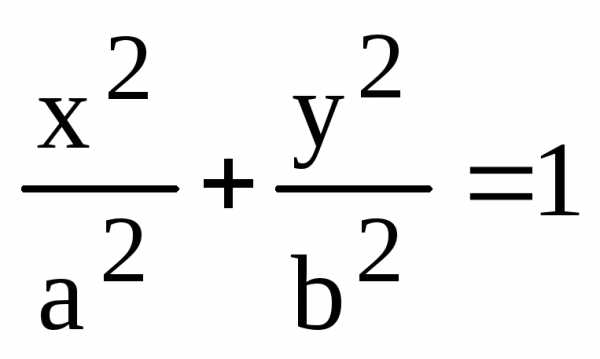. (4)

Доказательство. Доказательство проведем в два этапа. На первом этапе мы докажем, что координаты любой точки, лежащей на эллипсе удовлетворяют уравнению (4). На втором этапе мы докажем, что любое решение уравнения (4) дает координаты точки, лежащей на эллипсе. Отсюда будет следовать, что уравнению (4) удовлетворяют те и только те точки координатной плоскости, которые лежат на эллипсе. Отсюда и из определения уравнения кривой будет следовать, что уравнение (4) является уравнением эллипса.

1) Пусть точка М(х, у) является точкой эллипса, т.е. сумма ее фокальных радиусов равна 2а:

.

Воспользуемся формулой расстояния между двумя точками на координатной плоскости и найдем по этой формуле фокальные радиусы данной точки М:

, , откуда получаем:

.

Перенесем один корень в правую часть равенства и возведем в квадрат:

.

Сокращая, получаем:

.

Приводим подобные, сокращаем на 4 и уединяем радикал:

.

Возводим в квадрат

.

Раскрываем скобки и сокращаем на :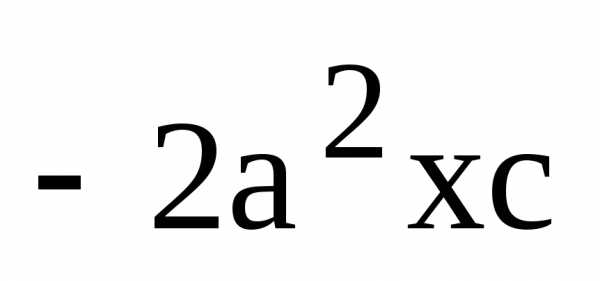

,

откуда получаем:

.

Используя равенство (2), получаем:

.

Разделив последнее равенство на 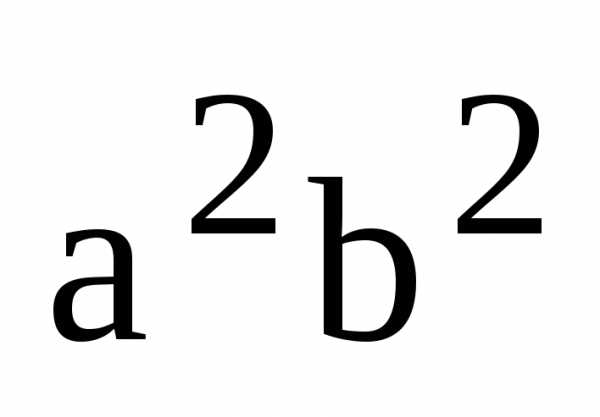, получаем равенство (4), ч.т.д.

2) Пусть теперь пара чисел (х, у) удовлетворяет уравнению (4) и пусть М(х, у) – соответствующая точка на координатной плоскости Оху.

Тогда из (4) следует:

.

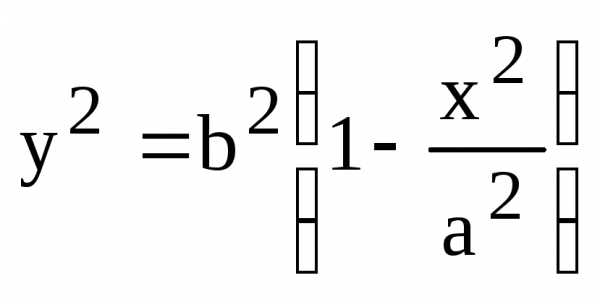Подставляем это равенство в выражение для фокальных радиусов точки М:

.

Здесь мы воспользовались равенством (2) и (3).

Таким образом, . Аналогично, .

Теперь заметим, что из равенства (4) следует, что

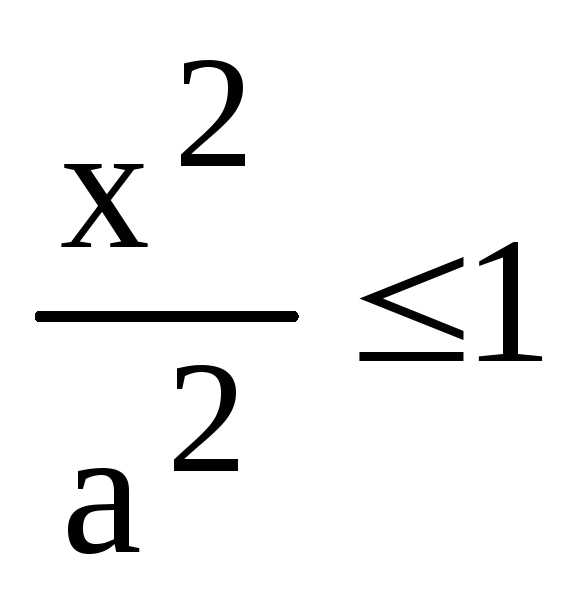или 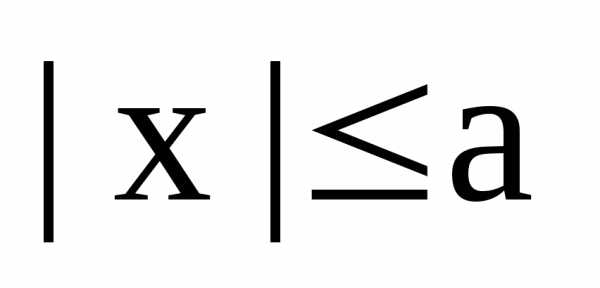и т.к. 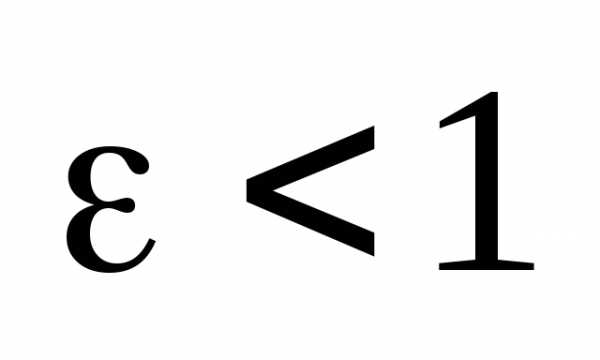, то отсюда следует неравенство:

.

Отсюда, в свою очередь, следует, что

или и

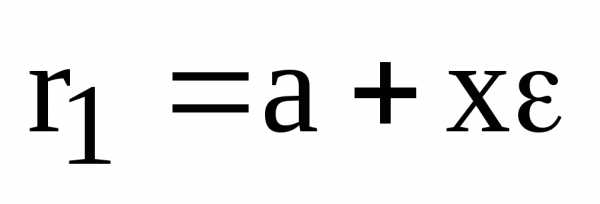, . (5)

Из равенств (5) следует, что , т.е. точка М(х, у) является точкой эллипса, ч.т.д.

Теорема доказана.

Определение. Уравнение (4) называется каноническим уравнением эллипса.

Определение. Канонические для эллипса оси координат называются главными осями эллипса.

Определение. Начало канонической для эллипса системы координат называется центром эллипса.

п.3. Свойства эллипса.

Теорема. (Свойства эллипса.)

1. В канонической для эллипса системе координат, все

точки эллипса находятся в прямоугольнике

, .

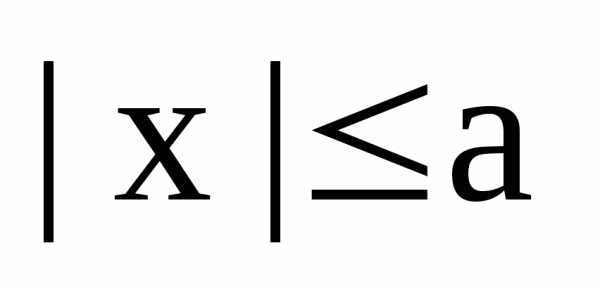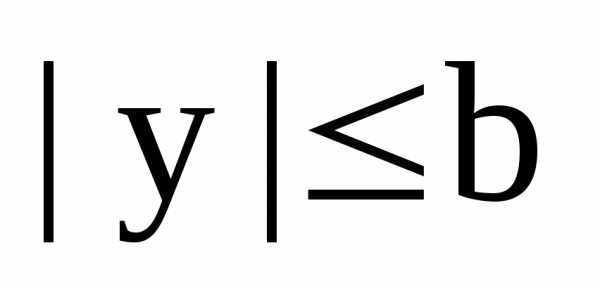2. Точки лежат на

эллипсе.

3. Эллипс является кривой, симметричной относительно

своих главных осей.

4. Центр эллипса является его центром симметрии.

Доказательство. 1, 2) Сразу же следует из канонического уравнения эллипса.

3, 4) Пусть М(х, у) – произвольная точка эллипса. Тогда ее координаты удовлетворяют уравнению (4). Но тогда координаты точек также удовлетворяют уравнению (4), и, следовательно, являются точками эллипса, откуда и следуют утверждения теоремы.

Теорема доказана.

рис.3.

Определение. Величина 2а называется большой осью эллипса, величина а называется большой полуосью эллипса.

Определение. Величина 2b называется малой осью эллипса, величина b называется малой полуосью эллипса.

Определение. Точки пересечения эллипса с его главными осями называются вершинами эллипса.

Замечание. Эллипс можно построить следующим образом. На плоскости в фокусы «забиваем по гвоздю» и закрепляем на них нить длиной 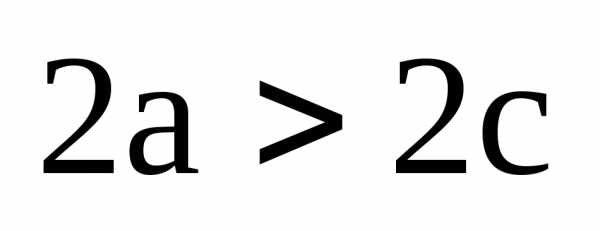. Затем берем карандаш и с его помощью натягиваем нить. Затем передвигаем карандашный грифель по плоскости, следя за тем, чтобы нить была в натянутом состоянии.

Из определения эксцентриситета следует, что

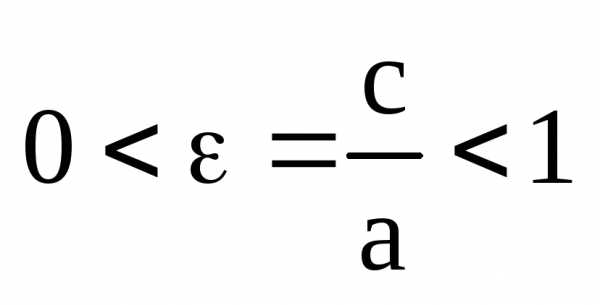
Зафиксируем число а и устремим число с к нулю. Тогда при , и . В пределе мы получаем

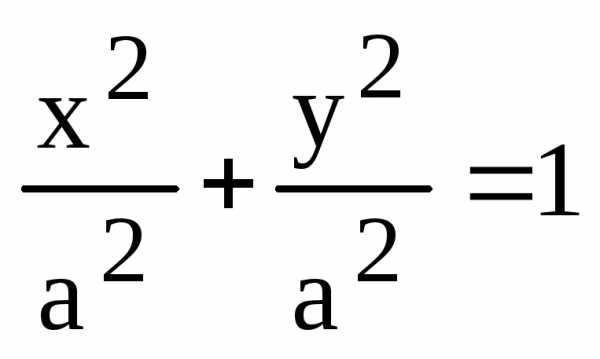или – уравнение окружности.

Таким образом, мы можем считать, что окружность есть эллипс с нулевым эксцентриситетом.

Устремим теперь 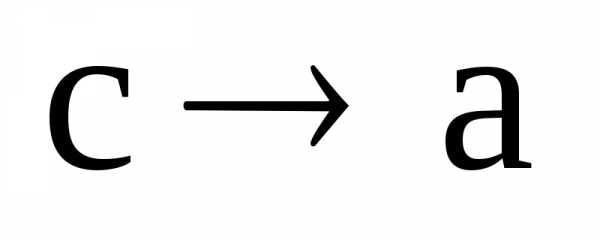. Тогда 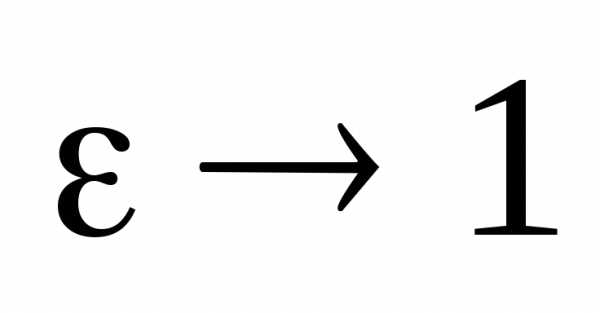, и мы видим, что в пределе эллипс вырождается в отрезок прямой в обозначениях рисунка 3.

п.4. Параметрические уравнения эллипса.

Теорема. Пусть 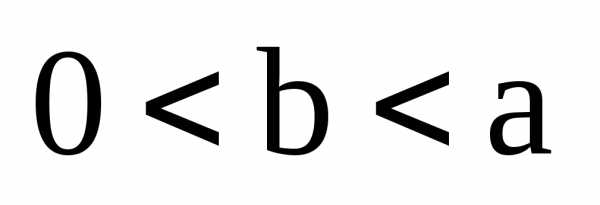– произвольные действительные числа. Тогда система уравнения

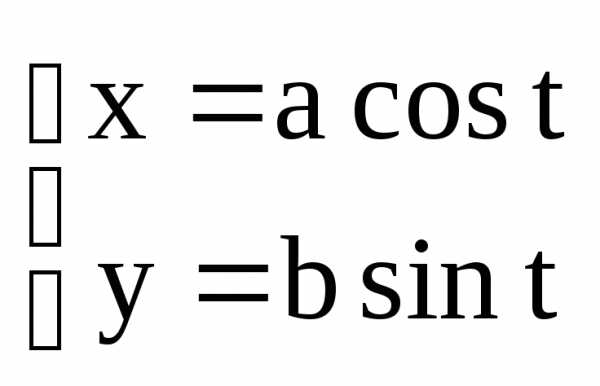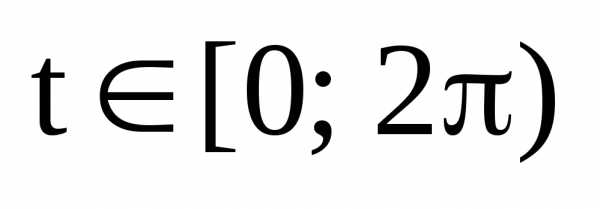, (6)

является параметрическими уравнениями эллипса в канонических для эллипса системе координат.

Доказательство. Достаточно доказать, что система уравнений (6) равносильна уравнению (4), т.е. они имеют одно и то же множество решений.

1) Пусть (х, у) – произвольное решение системы (6). Разделим первое уравнение на а, второе – на b, возводим оба уравнения в квадрат и складываем:

.

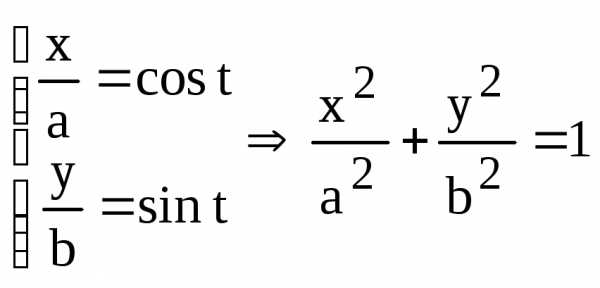Т.е. любое решение (х, у) системы (6) удовлетворяет уравнению (4).

2) Обратно, пусть пара (х, у) является решением уравнения (4), т.е.

.

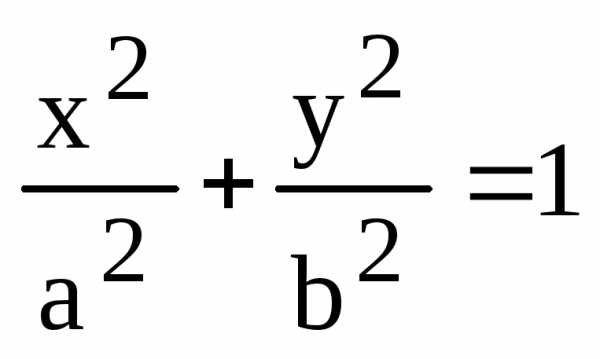Из этого равенства следует, что точка с координатами 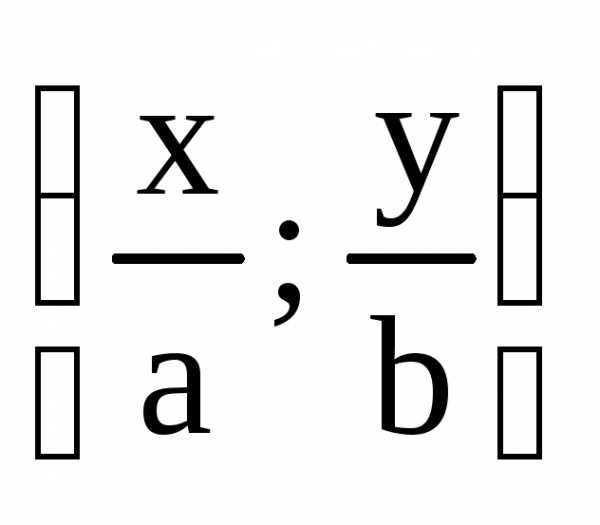лежит на окружности единичного радиуса с центром в начале координат, т.е. является точкой тригонометрической окружности, которой соответствует некоторый угол :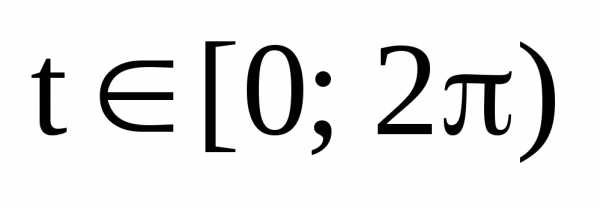

рис.4.

Из определения синуса и косинуса сразу же следует, что

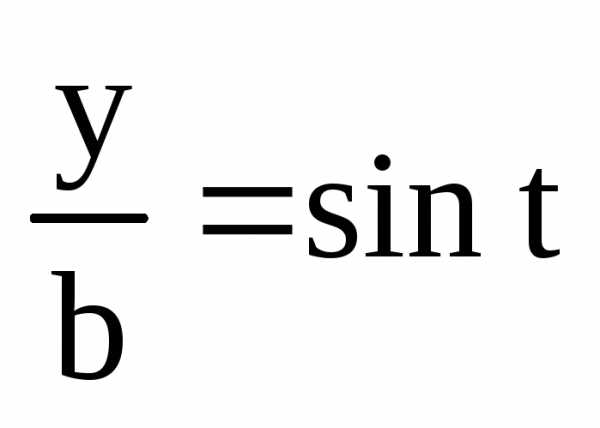, , где 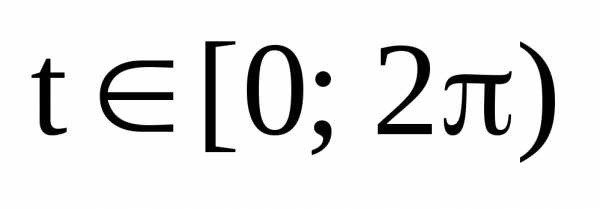, откуда и следует, что пара (х, у) является решением системы (6), ч.т.д.

Теорема доказана.

Замечание. Эллипс можно получить в результате равномерного «сжатия» окружности радиуса а к оси абсцисс.

Пусть – уравнение окружности с центром в начале координат. «Сжатие» окружности к оси абсцисс есть ни что иное, как преобразование координатной плоскости, осуществляемое по следующему правилу. Каждой точке М(х, у) поставим в соответствие точку этой же плоскости 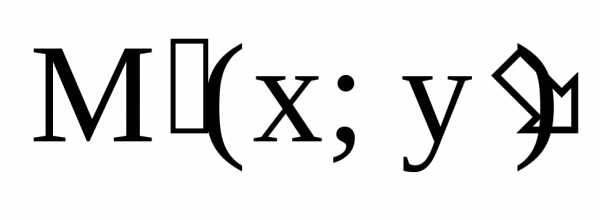, где 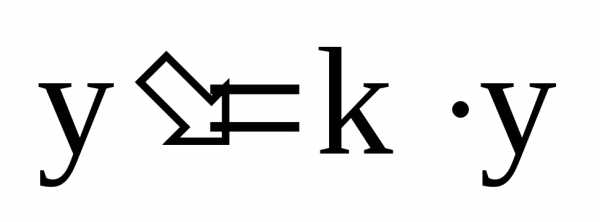, 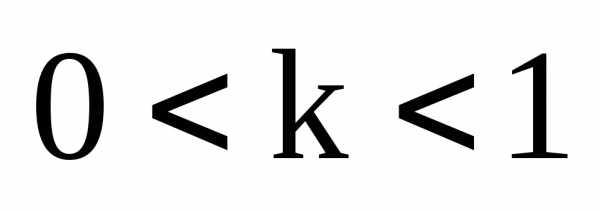– коэффициент «сжатия».

рис.5.

При этом преобразовании каждая точка окружности «переходит» в другую точку плоскости, имеющую ту же самую абсциссу, но меньшую ординату. Выразим старую ординату точки через новую:

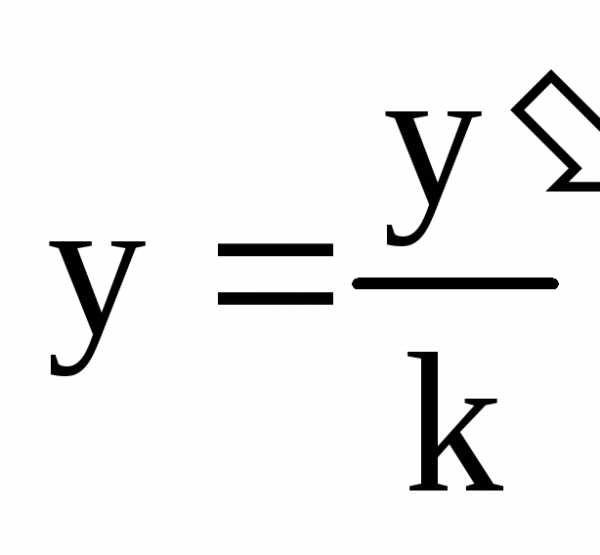
и подставим в уравнение окружности:

.

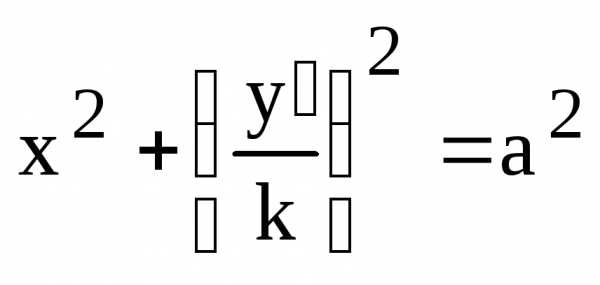Отсюда получаем:

. (7)

Отсюда следует, что если до преобразования «сжатия» точка М(х, у) лежала на окружности, т.е. ее координаты удовлетворяли уравнению окружности, то после преображования «сжатия» эта точка «перешла» в точку 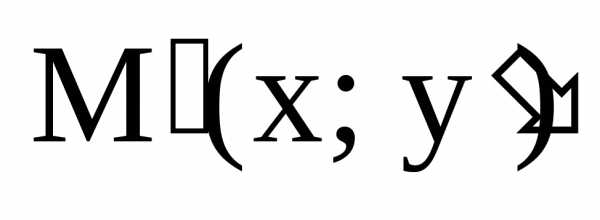, координаты которой удовлетворяют уравнению эллипса (7). Если мы хотим получить уравнение эллипса с малой полуосью b, то нужно взять коэффициент сжатия

.

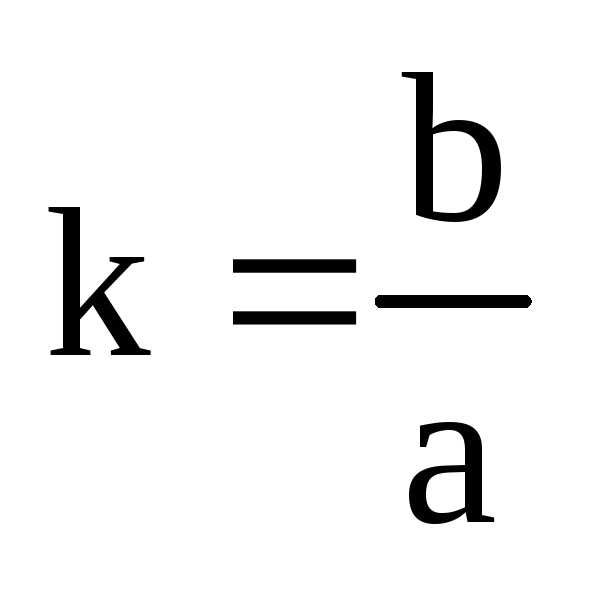рис.6.

п.5. Касательная к эллипсу.

Теорема. Пусть – произвольная точка эллипса

.

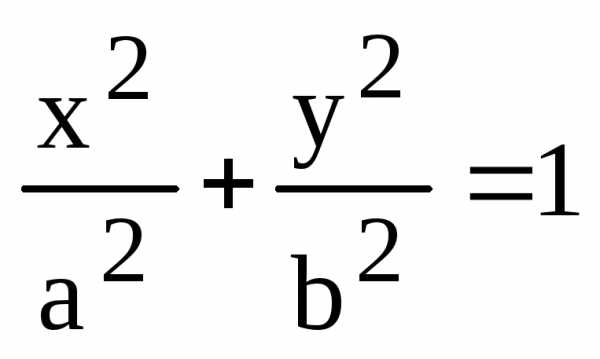Тогда уравнение касательной к этому эллипсу в точке имеет вид:

. (8)

Доказательство. Достаточно рассмотреть случай, когда точка касания лежит в первой или второй четверти координатной плоскости: . Уравнение эллипса в верхней полуплоскости имеет вид:

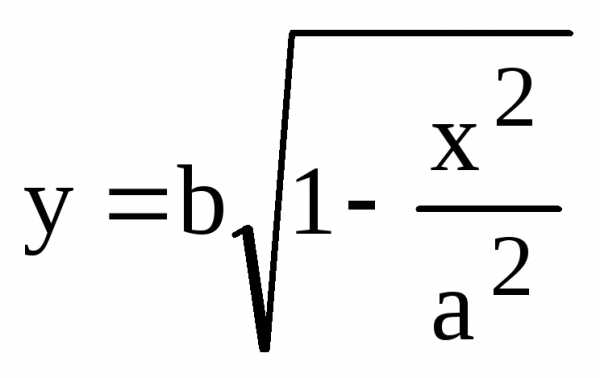. (9)

Воспользуемся уравнением касательной к графику функции 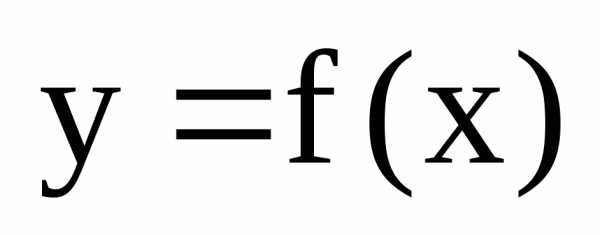в точке :

, (10)

где 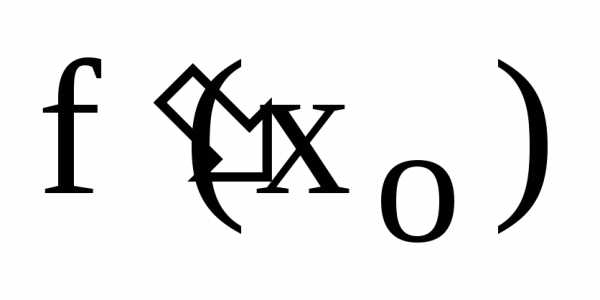– значение производной данной функции в точке . Эллипс в первой четверти можно рассматривать как график функции (8). Найдем ее производную и ее значение в точке касания:

,

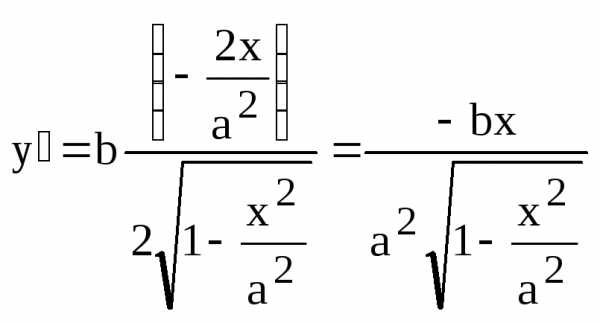. Здесь мы воспользовались тем, что точка касания является точкой эллипса и поэтому ее координаты удовлетворяют уравнению эллипса (9), т.е.

.

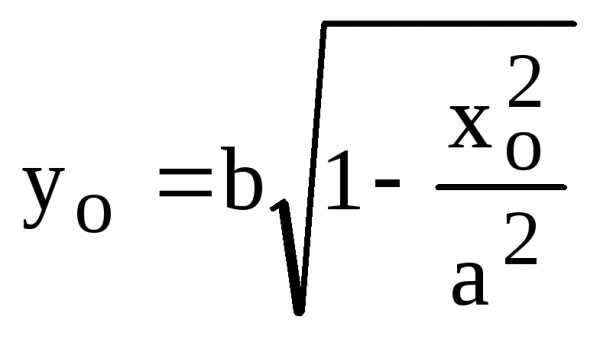Подставляем найденное значение производной в уравнение касательной (10):

,

откуда получаем:

или

.

Отсюда следует:

.

Разделим это равенство на :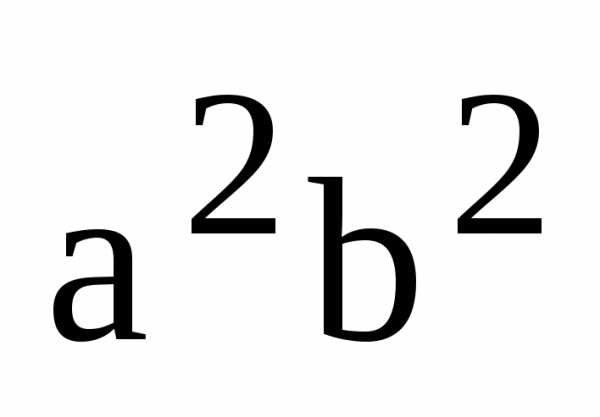

.

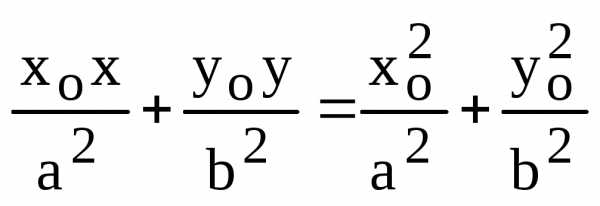Осталось заметить, что 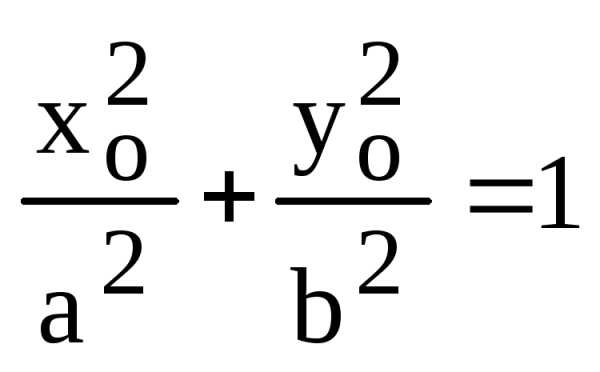, т.к. точка принадлежит эллипсу и ее координаты удовлетворяют его уравнению.

Аналогично доказывается уравнение касательной (8) в точке касания, лежащей в третьей или четвертой четверти координатной плоскости.

И, наконец, легко убеждаемся, что уравнение (8) дает уравнение касательной в точках , :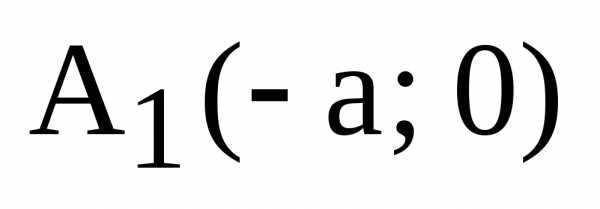

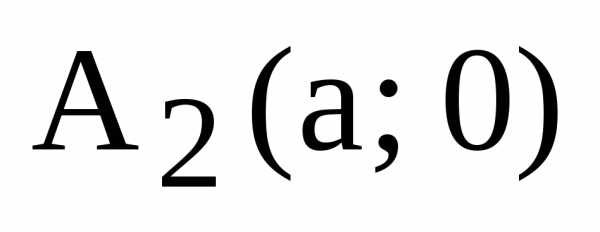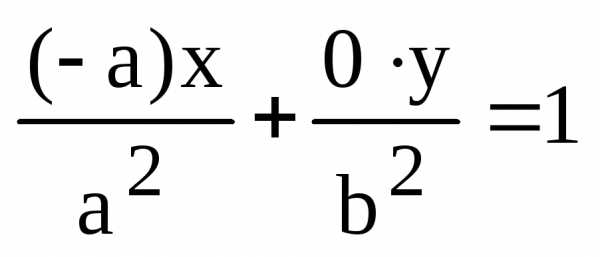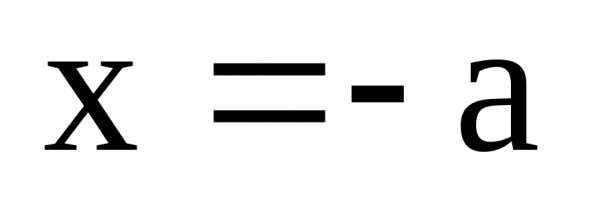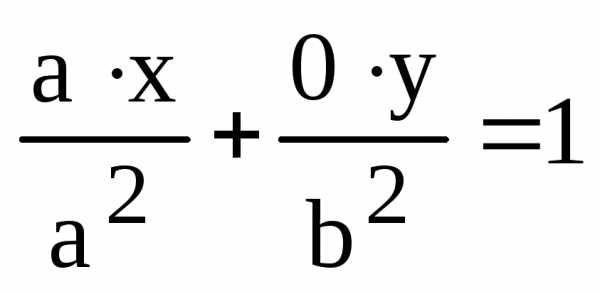или , и или .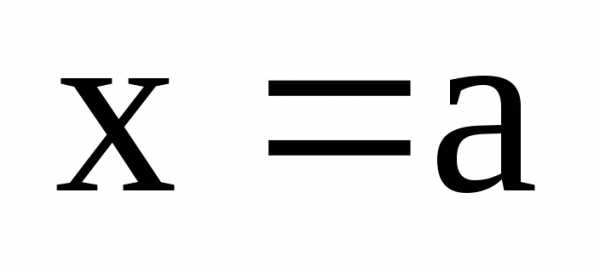

Теорема доказана.

п.6. Зеркальное свойство эллипса.

Теорема. Касательная к эллипсу имеет равные углы с фокальными радиусами точки касания.

рис.7.

Пусть – точка касания, , 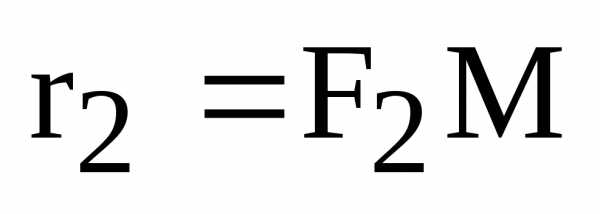– фокальные радиусы точки касания, Р и Q – проекции фокусов на касательную, проведенную к эллипсу в точке .

Теорема утверждает, что

. (11)

Это равенство можно интерпретировать как равенство углов падения и отражения луча света от эллипса, выпущенного из его фокуса. Это свойство получило название зеркального свойства эллипса:

Луч света, выпущенный из фокуса эллипса, после отражения от зеркала эллипса проходит через другой фокус эллипса.

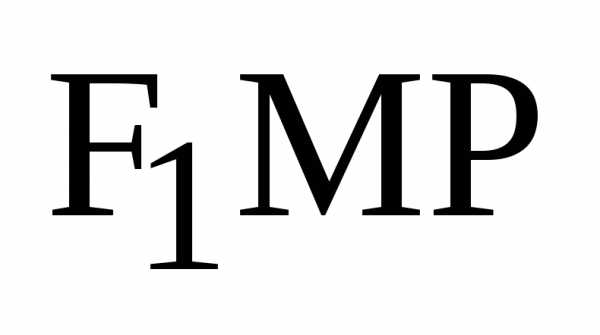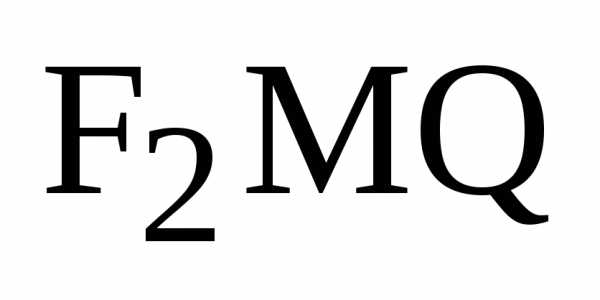Доказательство теоремы. Для доказательства равенства углов (11) мы докажем подобие треугольников и , в которых стороны и 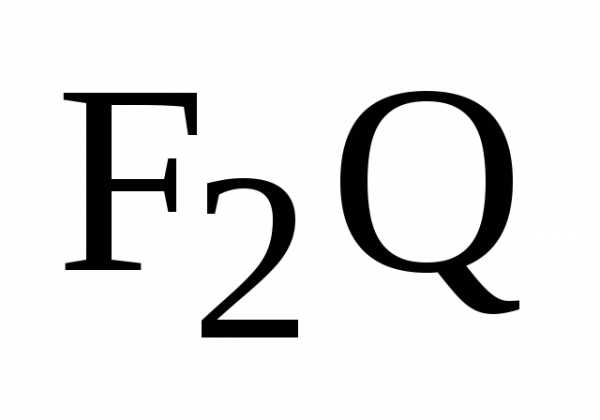будут сходственными. Так как треугольники прямоугольные, то достаточно доказать равенство

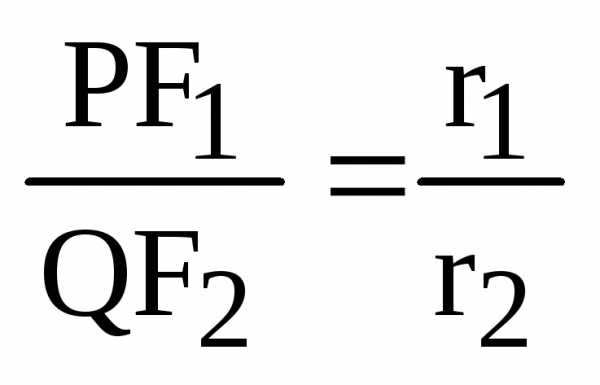. (12)

Так как по построению – расстояние от фокуса до касательной L (см. рис.7), . Воспользуемся формулой расстояния от точки до прямой на плоскости:

.

Так как уравнение касательной к эллипсу в точке имеет вид

,

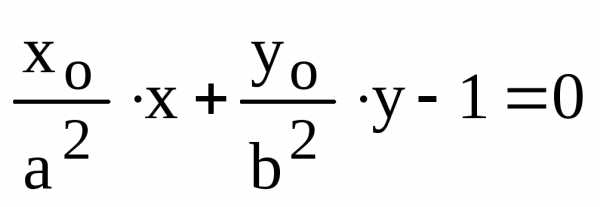то

,

и

.

Здесь мы воспользовались формулами (5) для фокальных радиусов точки эллипса.

Теорема доказана.

Второе доказательство теоремы:

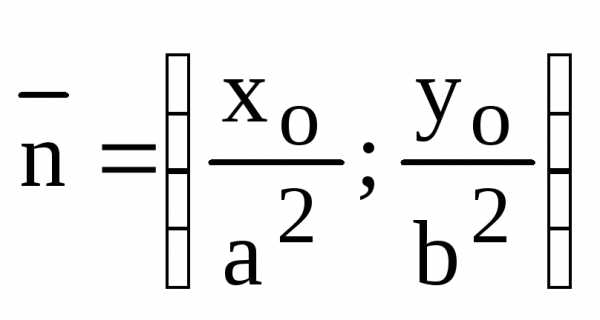, , – нормальный вектор касательной L.

. Отсюда, .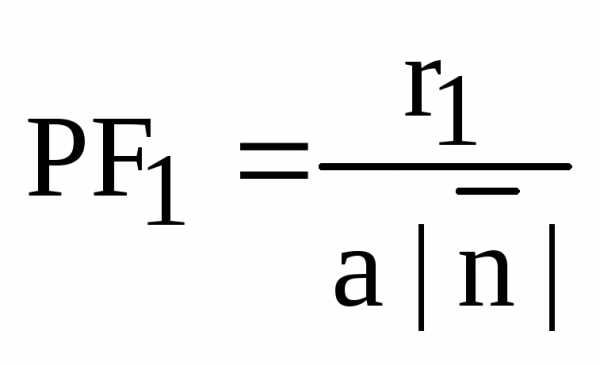

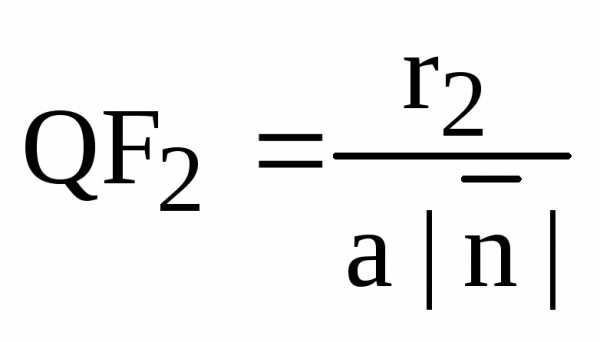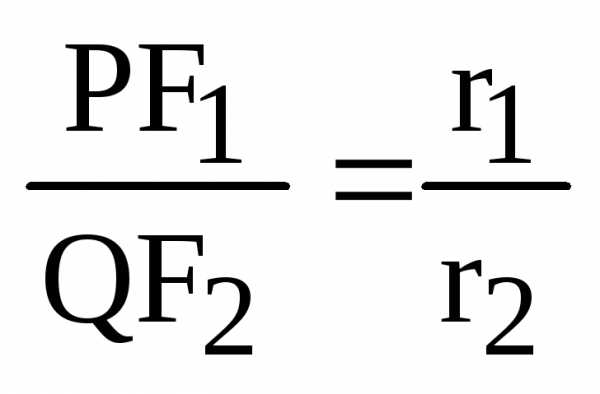Аналогично находим, и , ч.т.д.

п.7. Директрисы эллипса.

Определение. Директрисами эллипса называются две прямые, которые в канонической для эллипса системе координат имеют уравнения

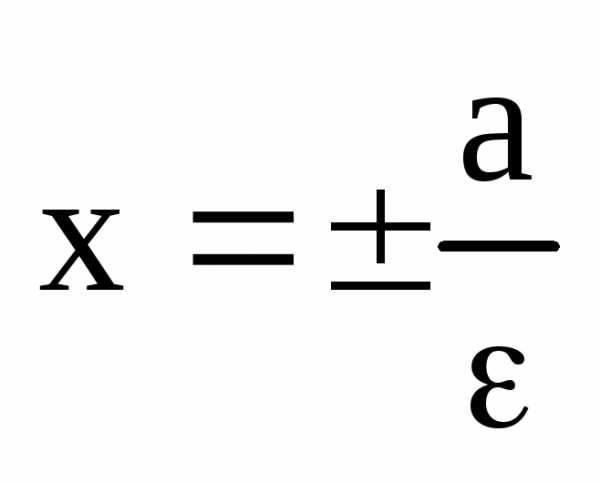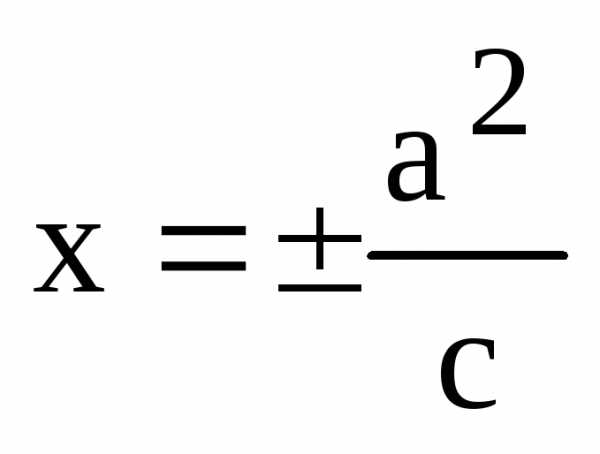или . (13)

рис.8.

Теорема. Пусть М – произвольная точка эллипса, , 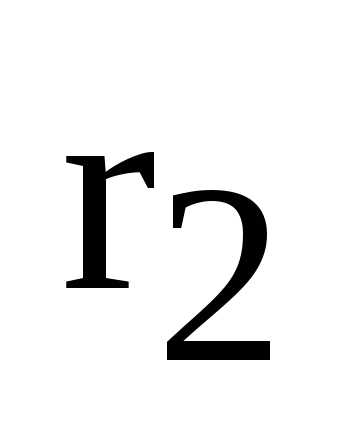– ее фокальные радиусы, 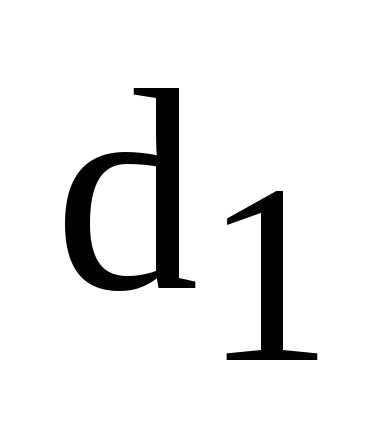– расстояние от точки М до левой директрисы, 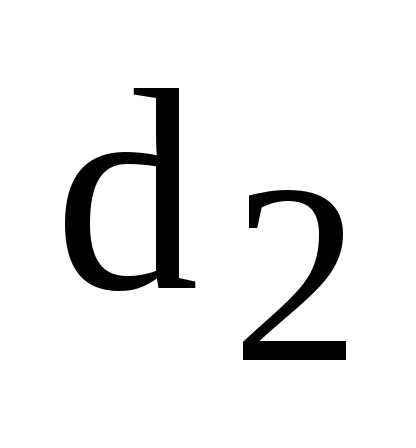– до правой. Тогда

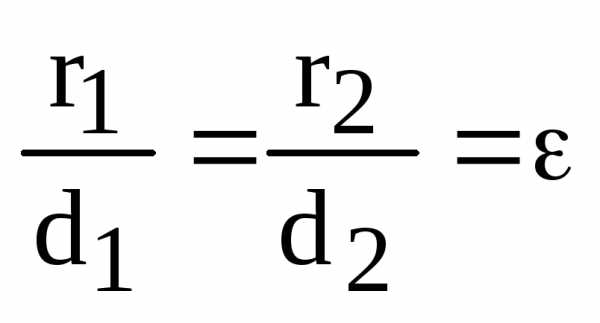, (14)

где – эксцентриситет эллипса.

Доказательство.

рис.9.

Пусть М(х, у) – координаты произвольной точки эллипса. Тогда

, ,

откуда и следуют равенства (14).

Теорема доказана.

п.8. Фокальный параметр эллипса.

Определение. Фокальным параметром эллипса называется длина перпендикуляра, восстановленного в его фокусе до пересечения с эллипсом.

Фокальный параметр принято обозначать буквой р.

рис.9.

Из определения следует, что фокальный параметр

.

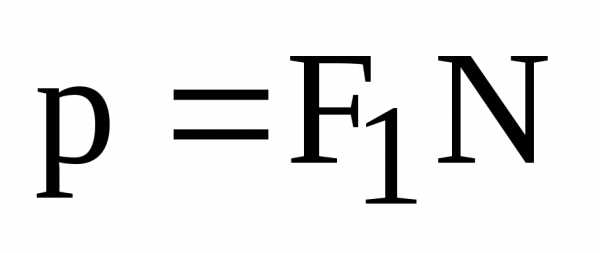Теорема. Фокальный параметр эллипса равен

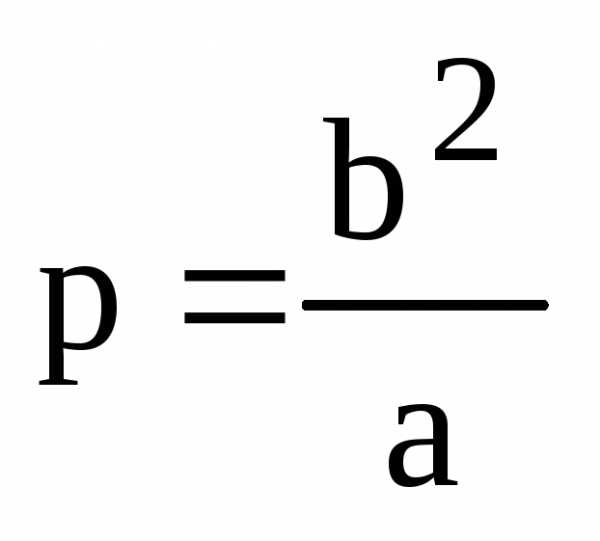. (15)

Доказательство. Так как точка N(–с; р) явяляется точкой эллипса 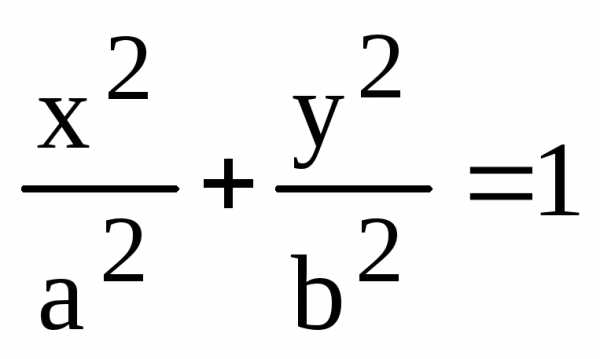, то ее координаты удовлетворяют его уравнению:

.

Отсюда находим

,

откуда и следует (15).

Теорема доказана.

п.9. Второе определение эллипса.

Теорема из п.7. может служить определением эллипса.

Определение. Эллипсом называется ГМТ для которых отношение расстояния до фиксированной точки плоскости, называемой фокусом, к расстоянию до фиксированной прямой, называемой директрисой, есть величина постоянная меньше единицы и называемая его эксцентриситетом:

.

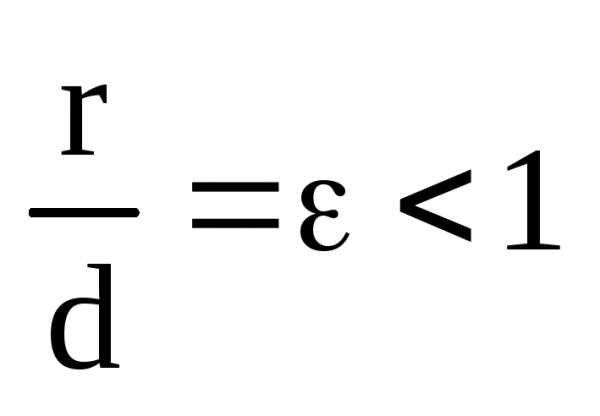рис.10.

Разумеется, в этом случае, первое определение эооипса является теоремой, которую необходимо доказывать.

studfiles.net

Эллипс

Творческая работа

Линии второго порядка

«Эллипс»

Выполнил: Егурнов Евгений

12 группа

Каноническое уравнение

Эллипс – это множество всех точек плоскости, сумма расстояний до каждой из которых от двух данных точек , называемых фокусами эллипса, – есть величина постоянная, численно равная длине большой оси этого эллипса: .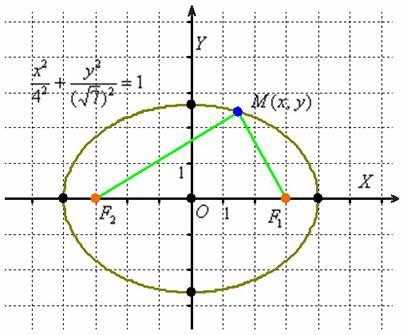 

Каноническое уравнение эллипса имеет вид  , где   – положительные действительные числа, причём . 

Пр. Эллипс задан уравнением 

Сначала приведём уравнение к каноническому виду:

Это позволит моментально определить вершины эллипса, которые находятся в точках . В данном случае : Отрезок  называют большой осью эллипса; отрезок  – малой осью; число  называют большой полуосью эллипса;  число  – малой полуосью.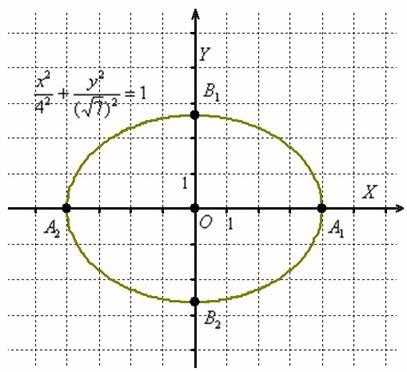

.

Любой эллипс симметричен относительно координатных осей, а также относительно начала координат.

Основное соотношение и частный случай

Эксцентриситетом эллипса называют отношение , которое может принимать значения в пределах .

Чем ближе значение эксцентриситета эллипса к единице, тем эллипс более продолговат.

Чем ближе значение эксцентриситета к нулю, тем эллипс больше похож на окружность.

Окружность – это частный случай эллипса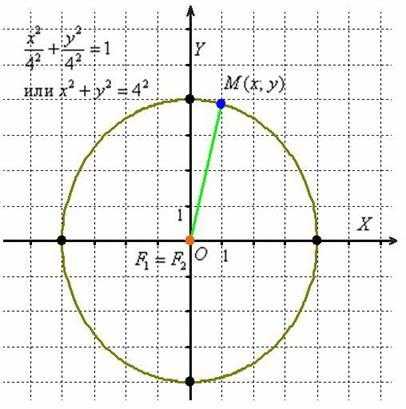

Действительно, в случае равенства полуосей каноническое уравнение эллипса принимает вид , который рефлекторно преобразуется к  – хорошо известному из школы уравнению окружности с центром в начале координат радиуса «а».

На практике чаще используют запись: . Радиусом называют длину отрезка , при этом каждая точка  окружности удалена от центра  на расстояние радиуса.

Заметьте, что определение эллипса остаётся полностью корректным: фокусы совпали , и сумма длин совпавших отрезков  для каждой точки окружности – есть величина постоянная. Так как расстояние между фокусами , то эксцентриситет  любой окружности равен нулю.

Директориальное свойство

Директрисами эллипса называются две прямые, проходящие параллельно оси ординат канонической системы координат на одинаковом расстоянии от нее. При , когда эллипс является окружностью, директрис нет (можно считать, что директрисы бесконечно удалены).

Эллипс с эксцентриситетом  можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки  (фокуса) к расстоянию до заданной прямой  (директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету  (директориальное свойство эллипса). Здесь  и  — один из фокусов эллипса и одна из его директрис, расположенные по одну сторону от оси ординат канонической системы координат, т.е.  или .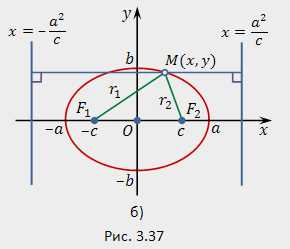

В самом деле, например, для фокуса  и директрисы  (рис.3.37,6) условие  можно записать в координатной форме:

Избавляясь от иррациональности и заменяя , приходим к каноническому уравнению эллипса. Аналогичные рассуждения можно провести для фокуса  и директрисы .

Оптическое свойство

Касательная эллипса образует в точке касания равные острые углы с фокальными радиусами.

Доказательство. Уравнение эллипса 

Для получения уравнения касательной продифференцируем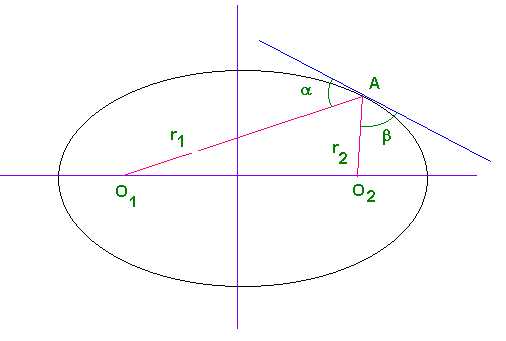 

Вектор, лежащий на касательной, 

 

= {a2y, b2x, 0}

 AO2

= {cx,y,0}

cos =			(     ,  O1A   ) a+x	,
cos =	(     ,  AO2   ) ax	. где  = c/a — эксцентриситет.

a2y(c+x)b2xy a+x

=

a2y(cx)+b2xy ax

a3xyab2xya2xyc=0

Преобразуем и получим

Сократим на axy, подставим  = c/a, получим тождество 

Литература

1. http://www.mathprofi.ru/linii_vtorogo_poryadka_ellips_i_okruzhnost.html

2. http://mathhelpplanet.com/static.php?p=ellips

3. http://vuz.exponenta.ru/PDF/optsvel.html

studfiles.net

Кривые второго порядка. Эллипс

Кривыми второго порядка на плоскости называются линии, определяемые уравнениями, в которых переменные координаты x и y содержатся во второй степени. К ним относятся эллипс, гипербола и парабола.

Общий вид уравнения кривой второго порядка следующий:

,

где A, B, C, D, E, F — числа и хотя бы один из коэффициентов A, B, C не равен нулю.

При решении задач с кривыми второго порядка чаще всего рассматриваются канонические уравнения эллипса, гиперболы и параболы. К ним легко перейти от общих уравнений, этому будет посвящён пример 1 задач с эллипсами.

Определение эллипса. Эллипсом называется множество всех точек плоскости, таких, для которых сумма расстояний до точек, называемых фокусами, есть величина постоянная и бОльшая, чем расстояние между фокусами.

Фокусы обозначены как и на рисунке ниже.

Каноническое уравнение эллипса имеет вид:

,

где a и b (a > b) — длины полуосей, т. е. половины длин отрезков, отсекаемых эллипсом на осях координат.

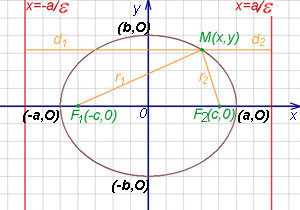
Прямая, проходящая через фокусы эллипса, является его осью симметрии. Другой осью симметрии эллипса является прямая, проходящая через середину отрезка перпендикулярно этому отрезку. Точка О пересечения этих прямых служит центром симметрии эллипса или просто центром эллипса.

Ось абсцисс эллипс пересекает в точках (a, О) и (- a, О), а ось ординат — в точках (b, О) и (- b, О). Эти четыре точки называются вершинами эллипса. Отрезок между вершинами эллипса на оси абсцисс называется его большой осью, а на оси ординат — малой осью. Их отрезки от вершины до центра эллипса называются полуосями.

Если a = b, то уравнение эллипса принимает вид . Это уравнение окружности радиуса a, а окружность — частный случай эллипса. Эллипс можно получить из окружности радиуса a, если сжать её в a/b раз вдоль оси Oy.

Пример 1. Проверить, является ли линия, заданная общим уравнением , эллипсом.

Решение. Производим преобразования общего уравнения. Применяем перенос свободного члена в правую часть, почленное деление уравнения на одно и то же число и сокращение дробей:

Ответ. Полученное в результате преобразований уравнение является каноническим уравнением эллипса. Следовательно, данная линия — эллипс.

Пример 2. Составить каноническое уравнение эллипса, если его полуоси соответственно равны 5 и 4.

Решение. Смотрим на формулу канонического уравения эллипса и подставляем: бОльшая полуось — это a = 5, меньшая полуось — это b = 4. Получаем каноническое уравнение эллипса:

.

---

---

Точки и , обозначенные зелёным на большей оси, где

,

называются фокусами.

Число

называется эксцентриситетом эллипса.

Отношение b/a характеризует «сплюснутость» эллипса. Чем меньше это отношение, тем сильнее эллипс вытянут вдоль большой оси. Однако степень вытянутости эллипса чаще принято выражать через эксцентриситет, формула которого приведена выше. Для разных эллипсов эксцентриситет меняется в пределах от 0 до 1, оставаясь всегда меньше единицы.

Пример 3. Составить каноническое уравнение эллипса, если расстояние между фокусами равно 8 и бОльшая ось равна 10.

Решение. Делаем несложные умозаключения:

— если бОльшая ось равна 10, то её половина, т. е. полуось a = 5,

— если расстояние между фокусами равно 8, то число c из координат фокусов равно 4.

Подставляем и вычисляем:

Результат — каноническое уравнение эллипса:

.

Пример 4. Составить каноническое уравнение эллипса, если его бОльшая ось равна 26 и эксцентриситет .

Решение. Как следует и из размера большей оси, и из уравнения эксцентриситета, бОльшая полуось эллипса a = 13. Из уравнения эсцентриситета выражаем число c, нужное для вычисления длины меньшей полуоси:

.

Вычисляем квадрат длины меньшей полуоси:

Составляем каноническое уравнение эллипса:

Пример 5. Определить фокусы эллипса, заданного каноническим уравнением .

Решение. Следует найти число c, определяющее первые координаты фокусов эллипса:

.

Получаем фокусы эллипса:

---

Если — произвольная точка эллипса (на чертеже обозначена зелёным в верхней правой части эллипса) и — расстояния до этой точки от фокусов , то формулы для расстояний — следующие:

.

Для каждой точки, принадлежащей эллипсу, сумма расстояний от фокусов есть величина постоянная, равная 2a.

Прямые, определяемые уравнениями

,

называются директрисами эллипса (на чертеже — красные линии по краям).

Пример 7. Дан эллипс . Составить уравнение его директрис.

Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет эллипса, т. е. . Все данные для этого есть. Вычисляем:

.

Получаем уравнение директрис эллипса:

Пример 8. Составить каноническое уравнение эллипса, если его фокусами являются точки , а директрисами являются прямые .

Решение. Смотрим в уравнение директрис, видим, что в нём можем заменить символ эксцентриситета формулой эксцентриситета как отношение первой координаты фокуса к длине большей полуоси. Так сможем вычислить квадрат длины большей полуоси. Получаем:

.

Теперь можем получить и квадрат длины меньшей полуоси:

Уравнение эллипса готово:

Пример 9. Проверить, находится ли точка на эллипсе . Если находится, найти расстояние от этой точки до фокусов эллипса.

Решение. Подставляем координаты точки x и y в уравнение эллипса, на выходе должно либо получиться равенство левой части уравнения единице (точка находится на эллипсе), либо не получиться это равенство (точка не находится на эллипсе). Получаем:

.

Получили единицу, следовательно, точка находится на эллипсе.

Приступаем к нахождению расстояния. Для этого нужно вычислить: число c, определяющее первые координаты фокусов, число e — эксцентриситет и числа «эр» с подстрочными индексами 1 и 2 — искомые расстояния. Получаем:

Проведём проверку: сумма расстояний от любой точки на эллипсе до фокусов должна быть равна 2a.

,

так как из исходного уравнения эллипса .

Одним из самых замечательных свойств эллипса является его оптическое свойство, состоящее в том, что прямые, соединяющие точку эллипса с его фокусами, пересекают касательную к эллипсу под разными углами. Это значит, что луч, пущенный из одного фокуса, после отраэения попадёт в другой. Это свойство лежит в основе аккустического эффекта, наблюдаемого в некоторых пещерах и искусственных сооружениях, своды которых имеют эллиптическую форму: если находиться в одном из фокусов, то речь человека, стоящего в другом фокусе, слышна так хорошо, как будто он находится рядом, хотя на самом деле расстояние велико.

Поделиться с друзьями

Другие материалы по теме Кривые второго порядка

function-x.ru

8.2. Каноническое уравнение эллипса и его характеристики

Эллипсом называется множество точек плоскости, сумма расстояний которых до двух данных точек , называемых фокусами, есть величина постояннаяРасстояние между фокусами эллипсаназывается фокусным расстоянием и обозначается

Общее уравнение эллипса

где большая полуось,малая полуось,координаты центра эллипса.

Если центр эллипса находится в начале координат и фокусы эллипса находятся на оси на равных расстояниях от начала координат, то уравнение примет вид

причем,

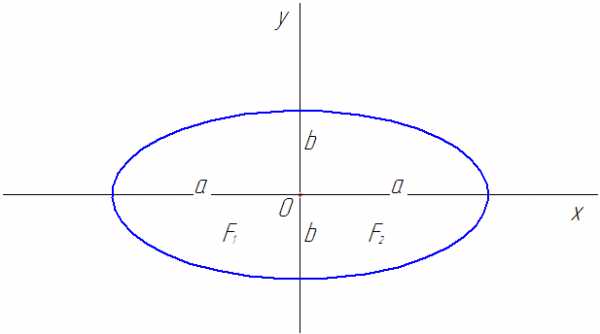
Рис. 13

Эллипс с центром в начале координат

Отношение фокусного расстояния к большой оси, т.е. называетсяэксцентриситетом (мера сжатия)

Эксцентриситет и коэффициент сжатия эллипсасвязаны соотношением

Директрисы эллипса.

Пусть дан эллипс

Рис. 14

Дирректрисы эллипса

с большой осью и эксцентриситетом

Отложим от центра эллипса на его большой оси отрезки

Прямые, проходящие через точки ипараллельно малой осиназываютсядиректрисами эллипса.

Для любой точки эллипса отношение ее расстояния до фокуса к расстоянию до соответствующей директрисы равно эксцентриситетут.е.

Рассмотрим пример. На эллипсе

найти точку, разность фокальных радиус-векторов которой равна 6,4.

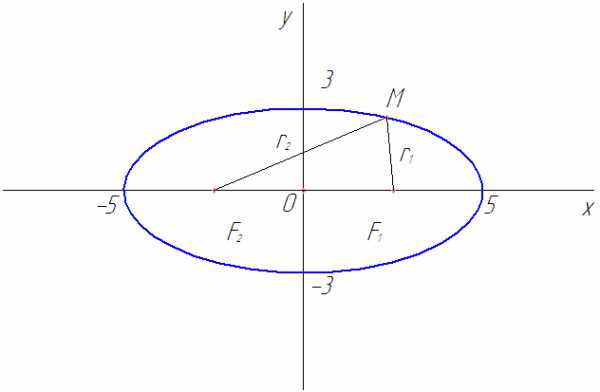
Рис. 15

Согласно уравнению эллипса определим расстояние от цента эллипса до фокусов

тогда

Кроме того,

Составим систему и решим ее

Получим

так как

Вывод: таких точек может быть две

8.3. Каноническое уравнение гиперболы и ее характеристики

Гиперболой называется множество всех точек плоскости, абсолютная величина разности расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная причем эта постоянная меньше расстояния между фокусами. Если поместить фокусы гиперболы в точкахто получается каноническое уравнение гиперболы

где Вершинами гиперболы являются точкитогдадействительная ось гиперболы,мнимая ось гиперболы.

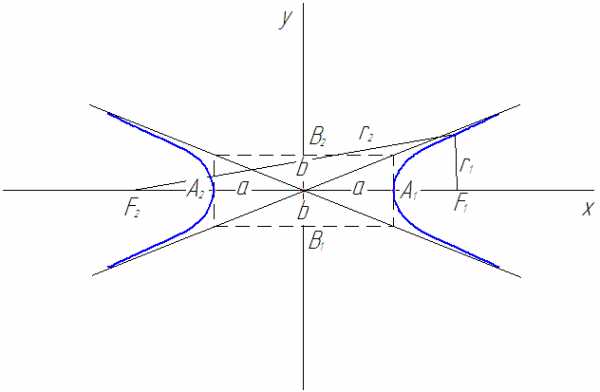
Рис. 16

Гипербола

Гипербола имеет две асимптоты

Эксцентриситет гиперболы

Фокальные радиус-векторы левой ветви гиперболы:

Фокальные радиус-векторы правой ветви гиперболы:

Рассмотрим пример. Найти уравнение гиперболы, вершины и фокусы которой находятся в соответствующих фокусах и вершинах эллипса

Найдем координаты фокусов, в которых лежат вершины гиперболы

следовательно

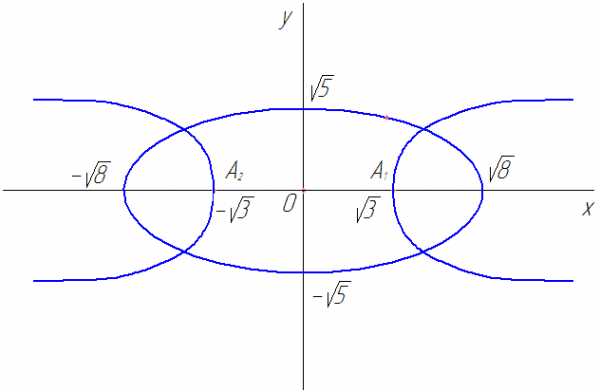
Рис. 17

Вершины гиперболы лежат в фокусах эллипса, следовательно

фокусы гиперболы, т.е.

Тогда

— уравнение гиперболы.

8.4. Каноническое уравнение параболы и ее характеристики

Парабола – это множество всех точек плоскости, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой. Если директрисой параболы является прямая а фокусом является точкато уравнение параболы имеет вид

Парабола симметрична относительно оси абсцисс

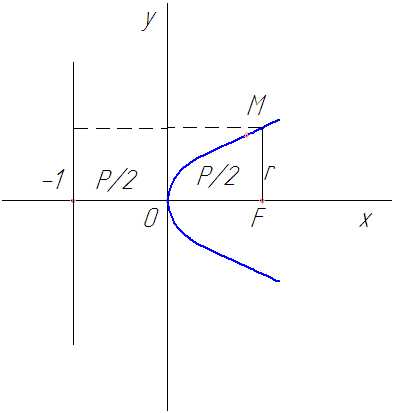
Рис. 18

Парабола

Рассмотрим пример. Составить простейшее уравнение параболы, если известно, что ее фокус находится в точке пересечения прямой и осью

В точке пересечения с осью координататогда

следовательно, фокус параболы.

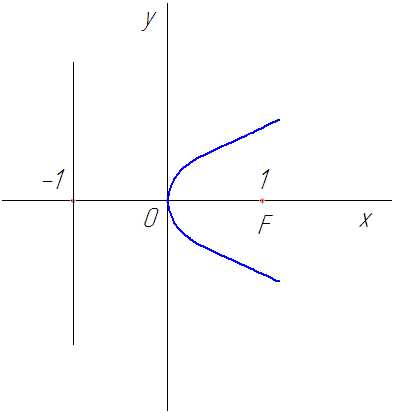
Рис. 19

Парабола

Парабола симметрична Так как

Тогда искомое уравнение параболы.

studfiles.net