Эллипсоид — это… Что такое Эллипсоид?
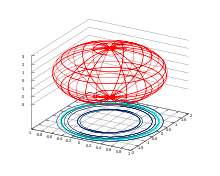 Эллипсоид вращения
Эллипсоид вращенияЭллипсо́ид — поверхность в трёхмерном пространстве, полученная деформацией сферы вдоль трёх взаимно перпендикулярных осей. Каноническое уравнение эллипсоида в декартовых координатах, совпадающих с осями деформации эллипсоида:
- где — произвольные положительные числа.
Величины a, b, c называют полуосями эллипсоида. Также эллипсоидом называют тело, ограниченное поверхностью эллипсоида. Эллипсоид представляет собой одну из возможных форм поверхностей второго порядка.

В случае, когда пара полуосей имеет одинаковую длину, эллипсоид может быть получен вращением эллипса вокруг одной из его осей. Такой эллипсоид называют эллипсоидом вращения или сфероидом.
Эллипсоид более точно, чем сфера, отражает идеализированную поверхность Земли.
Объём эллипсоида:
Площадь поверхности эллипсоида вращения:
Литература
- Киселёв В. Ю., Пяртли А. С., Калугина Т. Ф. Высшая математика. Первый семестр / интерактивный компьютерный учебник.
dic.academic.ru
Эллипсоид
Эллипсоид (рис.7) (от «эллипс»
и греч. «eidos» — вид) — замкнутая
центральная поверхность
второго порядка. Эллипсоид имеет
центр симметрии – 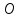 и три оси симметрии, которые называются
осями. Точки пересечения координатных
осей с эллипсоидом называются его
вершинами. Сечения эллипсоида плоскостями
являются эллипсами (в частности, всегда
можно указать круговые сечения эллипсоида).
Каноническое уравнение эллипсоида имеет
вид:
и три оси симметрии, которые называются
осями. Точки пересечения координатных
осей с эллипсоидом называются его
вершинами. Сечения эллипсоида плоскостями
являются эллипсами (в частности, всегда
можно указать круговые сечения эллипсоида).
Каноническое уравнение эллипсоида имеет
вид:
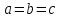 —
сфера.
—
сфера.
В сечении эллипсоида плоскостью, перпендикулярной любой из координатных осей, получается эллипс.
Форма эллипсоида.
Исследуем
форму эллипсоида. Из уравнения 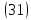 видно, что координаты точек поверхности
ограничены:
видно, что координаты точек поверхности
ограничены:
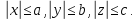
Эллипсоид обладает тремя плоскостями симметрии, тремя осями симметрии и центром симметрии. Ими служат соответственно координатные плоскости, координатные оси и начало координат.
Для
выяснения формы эллипсоида рассмотрим
его сечения плоскостями. Найдем линию
пересечения эллипсоида с плоскостью 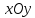
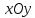 имеет
нулевую третью координату,
имеет
нулевую третью координату,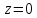 ,
то координаты точек эллипсоида на
плоскости
,
то координаты точек эллипсоида на
плоскости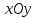 удовлетворяют
уравнению:
удовлетворяют
уравнению: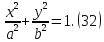
Получаем,
что линия пересечения является эллипсом
с полуосями 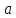 и
и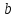
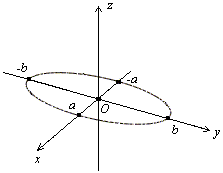
Аналогично,
сечение в плоскости 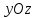 ,
дает эллипс:
,
дает эллипс:
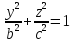
с
полуосями 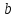 и
и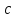 ,
а сечение плоскостью
,
а сечение плоскостью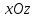 – эллипс:
– эллипс:
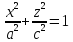
с
полуосями 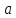 и
и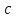
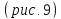
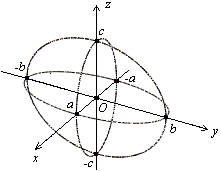
Рис.9. Сечения эллипсоида координатными плоскостями
Нарисованный
«каркас» из сечений уже дает
представление об эллипсоиде. Но чтобы
выяснить, как ведет себя поверхность
между нарисованными кривыми, рассмотрим
сечение эллипсоида плоскостью 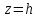 .
Эта плоскость параллельна плоскости
.
Эта плоскость параллельна плоскости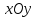 и
пересекает ось
и
пересекает ось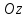 в
точке
в
точке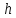 .
Уравнения этой линии:
.
Уравнения этой линии:
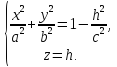
Очевидно,
что если 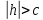 ,
то ни одна точка пространства не может
удовлетворять этой системе: в левой
части первого уравнения стоит
неотрицательное число, а в правой —
отрицательное.
,
то ни одна точка пространства не может
удовлетворять этой системе: в левой
части первого уравнения стоит
неотрицательное число, а в правой —
отрицательное.
Если 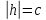 ,
то в сечении получим лишь одну точку
,
то в сечении получим лишь одну точку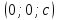 или
или в
зависимости от знака
в
зависимости от знака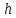 .
.
Пусть 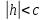 .
Тогда первое уравнение преобразуем к
виду:
.
Тогда первое уравнение преобразуем к
виду:
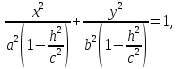
то есть к виду:
где 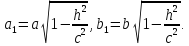
Уравнение 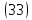 является уравнением эллипса, подобного
эллипсу, задаваемому уравнением
является уравнением эллипса, подобного
эллипсу, задаваемому уравнением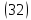 ,
с коэффициентом подобия
,
с коэффициентом подобия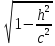 и
полуосями
и
полуосями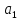 и
и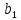 .
Ясно, что сечение плоскостью
.
Ясно, что сечение плоскостью
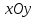 .
Нарисуем эти сечения
.
Нарисуем эти сечения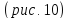 .
. 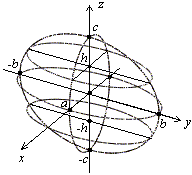
Рис.10. Дополнительные сечения эллипсоида
Таким
образом, весь эллипсоид составлен из
эллипсов, лежащих в плоскостях,
параллельных плоскости 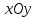 и
подобных эллипсу в плоскости
и
подобных эллипсу в плоскости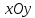 .
.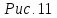 дает более привычное глазу изображение
эллипсоида:
дает более привычное глазу изображение
эллипсоида:
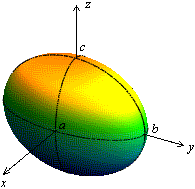
Рис.11. Эллипсоид
Так
же, как для эллипса, точки пересечения
эллипсоида с координатными осями
называются вершинами эллипсоида, центр
симметрии — центром эллипсоида. Числа 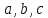 называются
полуосями. Если полуоси попарно различны,
то эллипсоид называется трехосным.
называются
полуосями. Если полуоси попарно различны,
то эллипсоид называется трехосным.
Если
две полуоси равны друг другу, то эллипсоид
называется эллипсоидом вращения.
Эллипсоид вращения может быть получен
вращением эллипса вокруг одной из осей.
Например, если 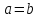 ,
то все сечения эллипсоида плоскостями
,
то все сечения эллипсоида плоскостями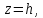
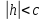 ,
будут окружностями. Сам эллипсоид может
быть получен из эллипса:
,
будут окружностями. Сам эллипсоид может
быть получен из эллипса:
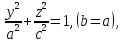
лежащего
в плоскости 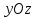 ,
при вращении его вокруг оси
,
при вращении его вокруг оси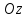
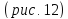 .
.

Рис.12. Эллипсоид вращения
studfile.net
Эллипсоид* — это… Что такое Эллипсоид*?
— Поверхность второго порядка, замкнутая, имеющая центр и пересекаемая всякой плоскостью по эллипсам или кругам, называется Э. На прилагаемом чертеже изображен Э. с тремя неравными главными взаимно перпендикулярными полуосями: большой а = OA, средней b = OB и малой с = ОС. Если начало координата взято в центре О Э., ось X-ов расположена по A’ОА, ось Y -ов по B’ОВ и ось Z -ов по C’OC, то уравнение Э. будет:Поверхность эта обладает, между прочим, следующими геометрическими свойствами. Если через какую-нибудь точку её провести касательную к ней плоскость, то пересечения всех плоскостей, ей параллельных, с поверхностью Э. будут эллипсы, подобные друг другу, с параллельными между собой большими главными осями и с параллельными между собой главными малыми осями.
Та плоскость, параллельная касательной плоскости, которая проходит через центр Э., называется диаметральной плоскостью, сопряженной диаметру, проведенному через центр и точку касания. Диаметры А’А, B’B, C’С называются главными диаметральными, а плоскости эллипсов CВC’В ‘, ACA’C’, ABA’B’ — главными диаметральными плоскостями. На главном диаметральном эллипсе АСА’C’ имеются четыре точки, расположенные на концах двух диаметров этого эллипса, наклоненных к оси Х-ов под углами, тангенсы которых равны
+ (с/a)√ [(b2—c2 )/(a2—b2)], — (с/a)√ [(b2—c2 )/(a2—b2)].
Точки эти называются точками закругления. Касательные плоскости к Э., проведенные в этих точках, параллельны оси Y -ов и, значит, перпендикулярны в плоскости XOZ. Плоскости, секущие Э. и параллельные этим плоскостям, дают не эллиптические, но круговые сечения. Те две проходящие через центр плоскости, которые сопряженны двум диаметрам точек закругления, пересекают Э. по двум кругам радиуса b, проходящим через ось Y -ов.
Э. инерции, вращение твердого тела вокруг неподвижной точки по uнepцuu.
В статье: Момент инерции (см.) было объяснено значение Э. инерции твердого тела для какой-либо точки и значение главных осей инерции.
Если А = ∑ m(y2 + z2), В = ∑m(z2 + x2), С = ∑ m(x2 + у 2) суть моменты инерции вокруг главных осей инерции, проведенных через рассматриваемую точку тела, то величины главных полуосей Э. инерции обратно пропорциональны корням квадратным из этих главных моментов инерции, т. е. a = (√A) —1, b = (√B)—1, c = (√C) —1, тогда уравнение Э. инерции принимает вид (1). Надо, однако, заметить, что не всякий Э. может быть Э. инерции; надо, чтобы величины полуосей а, b, с удовлетворяли некоторому условию. Можно убедиться, что: A + B — C = 2∑mz2 и, следовательно, эта величина всегда положительная; поэтому a2, b2 и с 2 должны удовлетворять условию:
(a2
) —1 + (b2 ) —1 — (c2) —1 > 0.Например, Э., полуоси которого суть а = 3, b = 2, с = 1 не может быть Э. инерции никакого тела, потому что 1/9 + 1/4 + —1<0.
В тех случаях, в которых Э. инерции есть Э. вращения, то есть когда b = a, то предыдущее условие обратится в следующее:
2/a
2 > 1/с 2,откуда с должно быть больше a/√2. Следовательно, Э. инерции может быть удлиненным Э. вращения при произвольной длине с, большей экваториальной полуоси а, но сжатый или планетарный Э. может быть Э. инерции, если малая полуось с не меньше экваториальной полуоси а, деленной на √2. Если твердому телу, имеющему неподвижную точку, сообщить какой-либо толчок, приводящий его во вращение вокруг этой точки, и если на тело не действуют никакие внешние силы, то вращение, совершаемое телом, называют вращением по инерции. При таком вращении живая сила вращательных движений всего тела остается постоянной; остается также постоянным и момент количества движения всего тела вокруг неподвижной точки (см.). Момент количества движений всего тела (так назыв. главный момент количества движений тела) может быть изображен линейно, в виде вектора (см.), т. е. длины, проведенной из неподвижной точки. Длина эта остается при вращении по инерции постоянной, и направление её остается в пространстве неизменным. Пуансо (см.) показал, что геометрический характер вращения твердого тела по инерции может быть выражен следующим образом. Тот Э. инерции твердого тела, центром которого служит неподвижная точка, катится без скольжения по двум плоскостям, перпендикулярным к главному моменту количества движения и находящимся на равных постоянных расстояниях по обе стороны неподвижной точки. При катании без скольжения мгновенная ось вращения (см.) проходит через точки прикосновения Э. к неподвижным плоскостям. Та кривая линия, которую описывает каждая из двух этих точек прикосновения на поверхности Э., называется noлoдиeю, a та кривая, которую эта точка описывает на неподвижной плоскости, называется эрполодиею. Величина расстояния выше сказанных плоскостей от неподвижной точки зависит от величины живой силы вращения твердого тела и от величины главного момента количества движения. Расстояния эти ни в каком случае не могут быть больше большой полуоси и меньше малой полуоси Э. инерции. Если расстояния эти равны большой, средней или малой полуоси этого Э., то полодии и эрполодии обращаются в точки. Тогда вращение по инерции твердого тела будет совершаться равномерно вокруг одной из главных осей Э. инерции, и самая ось будет сохранять неизменное направление в пространстве. По этой причине главные оси Э. инерции называются главными осями инерции. Когда Э. инерции есть Э. вращения, то полодии суть параллельные круги на Э. и эрполодии суть круги на неподвижных плоскостях. Вращение по инерции такого тела состоит из вращения вокруг оси симметрии Э., причем эта ось равномерно описывает прямой конус вокруг главного момента количества движения. Вращение это аналогично тому, которое описано в конце статьи Вращательное движение (см.).
Э. упругости и Э. деформаций. Ламе (см.) ввел в теорию упругости представление об Э. упругости. Напряжения сил упругости (см. Упругость), действующие на площадки, проходящие через одну и ту же точку упругого тела, имеют различные величины и направления в зависимости от направления нормали. Если изобразить напряжения, приложенные к площадкам всевозможных направлений (но проходящих через одну и ту же точку), длинами, отложенными по направлениям напряжений, то оконечности этих длин образуют поверхность Э. упругости. Ничтожно малые деформации, совершающиеся при переходе упругого тела из естественного состояния в деформированное, происходят так, что если вокруг какой-нибудь точки опишем шар весьма малого радиуса, то частицы, находившиеся в естественном состоянии внутри и на поверхности этого шара, в деформированном состоянии будут находиться внутри и на поверхности некоторого Э. Обратно, можно вокруг точки как вокруг центра описать такой Э., который при деформации обратится в шар; Э. этот называется Э. деформации.
Д. Б.
Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона. — С.-Пб.: Брокгауз-Ефрон. 1890—1907.
dic.academic.ru
Эллипсоид — это… Что такое Эллипсоид?
Поверхность второго порядка, замкнутая, имеющая центр и пересекаемая всякой плоскостью по эллипсам или кругам, называется Э. На прилагаемом чертеже изображен Э. с тремя неравными главными взаимно перпендикулярными полуосями: большой а = OA, средней b = OB и малой с = ОС. Если начало координата взято в центре О Э., ось Х-ов расположена по A’ОА, ось Y-ов по B’ОВ и ось Z-ов по C’OC, то уравнение Э. будет:
x2/a2 + y2/b2 + z2/c2 = 1. (1)
Поверхность эта обладает, между прочим, следующими геометрическими свойствами. Если через какую-нибудь точку её провести касательную к ней плоскость, то пересечения всех плоскостей, ей параллельных, с поверхностью Э. будут эллипсы, подобные друг другу, с параллельными между собой большими главными осями и с параллельными между собой главными малыми осями.
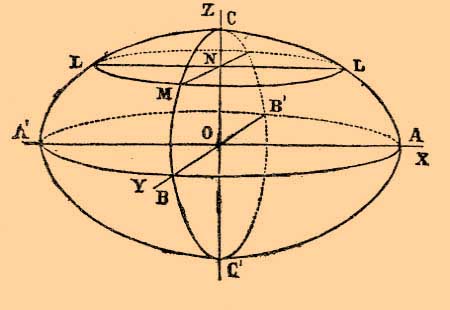
Та плоскость, параллельная касательной плоскости, которая проходит через центр Э., называется диаметральной плоскостью, сопряженной диаметру, проведенному через центр и точку касания. Диаметры А’А, B’B, C’С называются главными диаметральными, а плоскости эллипсов CBC’В‘, ACA’C’, ABA’B’ — главными диаметральными плоскостями. На главном диаметральном эллипсе АСА’C’ имеются четыре точки, расположенные на концах двух диаметров этого эллипса, наклоненных к оси Х-ов под углами, тангенсы которых равны
+ (с/a)√ [(b2—c2 )/(a2—b2)], — (с/a)√ [(b2—c2 )/(a2—b2)].
Точки эти называются точками закругления. Касательные плоскости к Э., проведенные в этих точках, параллельны оси Y-ов и, значит, перпендикулярны в плоскости XOZ. Плоскости, секущие Э. и параллельные этим плоскостям, дают не эллиптические, но круговые сечения. Те две проходящие через центр плоскости, которые сопряженны двум диаметрам точек закругления, пересекают Э. по двум кругам радиуса b, проходящим через ось Y-ов.
Э. инерции, вращение твердого тела вокруг неподвижной точки по инерции.
В статье: Момент инерции (см.) было объяснено значение Э. инерции твердого тела для какой-либо точки и значение главных осей инерции.
Если А = ∑ m(y2 + z2), В = ∑m(z2 + x2), С = ∑ m(x2 + у2) суть моменты инерции вокруг главных осей инерции, проведенных через рассматриваемую точку тела, то величины главных полуосей Э. инерции обратно пропорциональны корням квадратным из этих главных моментов инерции, т. е. a = (√A) —1, b = (√B)—1, c = (√C) —1, тогда уравнение Э. инерции принимает вид (1). Надо, однако, заметить, что не всякий Э. может быть Э. инерции; надо, чтобы величины полуосей а, b, с удовлетворяли некоторому условию. Можно убедиться, что: A + B — C = 2∑mz2 и, следовательно, эта величина всегда положительная; поэтому a2, b2 и с2 должны удовлетворять условию:
(a2) —1 + (b2 ) —1 — (c2) —1 > 0.
Например, Э., полуоси которого суть а = 3, b = 2, с = 1 не может быть Э. инерции никакого тела, потому что 1/9 + 1/4 + —1В тех случаях, в которых Э. инерции есть Э. вращения, то есть когда b = a, то предыдущее условие обратится в следующее:
2/a2 > 1/с2,
откуда с должно быть больше a/√2. Следовательно, Э. инерции может быть удлиненным Э. вращения при произвольной длине с, большей экваториальной полуоси а, но сжатый или планетарный Э. может быть Э. инерции, если малая полуось с не меньше экваториальной полуоси а, деленной на √2. Если твердому телу, имеющему неподвижную точку, сообщить какой-либо толчок, приводящий его во вращение вокруг этой точки, и если на тело не действуют никакие внешние силы, то вращение, совершаемое телом, называют вращением по инерции. При таком вращении живая сила вращательных движений всего тела остается постоянной; остается также постоянным и момент количества движения всего тела вокруг неподвижной точки (см.). Момент количества движений всего тела (так назыв. главный момент количества движений тела) может быть изображен линейно, в виде вектора (см.), т. е. длины, проведенной из неподвижной точки. Длина эта остается при вращении по инерции постоянной, и направление её остается в пространстве неизменным. Пуансо (см.) показал, что геометрический характер вращения твердого тела по инерции может быть выражен следующим образом. Тот Э. инерции твердого тела, центром которого служит неподвижная точка, катится без скольжения по двум плоскостям, перпендикулярным к главному моменту количества движения и находящимся на равных постоянных расстояниях по обе стороны неподвижной точки. При катании без скольжения мгновенная ось вращения (см.) проходит через точки прикосновения Э. к неподвижным плоскостям. Та кривая линия, которую описывает каждая из двух этих точек прикосновения на поверхности Э., называется полодиею, a та кривая, которую эта точка описывает на неподвижной плоскости, называется эрполодиею. Величина расстояния выше сказанных плоскостей от неподвижной точки зависит от величины живой силы вращения твердого тела и от величины главного момента количества движения. Расстояния эти ни в каком случае не могут быть больше большой полуоси и меньше малой полуоси Э. инерции. Если расстояния эти равны большой, средней или малой полуоси этого Э., то полодии и эрполодии обращаются в точки. Тогда вращение по инерции твердого тела будет совершаться равномерно вокруг одной из главных осей Э. инерции, и самая ось будет сохранять неизменное направление в пространстве. По этой причине главные оси Э. инерции называются главными осями инерции. Когда Э. инерции есть Э. вращения, то полодии суть параллельные круги на Э. и эрполодии суть круги на неподвижных плоскостях. Вращение по инерции такого тела состоит из вращения вокруг оси симметрии Э., причем эта ось равномерно описывает прямой конус вокруг главного момента количества движения. Вращение это аналогично тому, которое описано в конце статьи Вращательное движение (см.).
Э. упругости и Э. деформаций. Ламе (см.) ввел в теорию упругости представление об Э. упругости. Напряжения сил упругости (см. Упругость), действующие на площадки, проходящие через одну и ту же точку упругого тела, имеют различные величины и направления в зависимости от направления нормали. Если изобразить напряжения, приложенные к площадкам всевозможных направлений (но проходящих через одну и ту же точку), длинами, отложенными по направлениям напряжений, то оконечности этих длин образуют поверхность Э. упругости. Ничтожно малые деформации, совершающиеся при переходе упругого тела из естественного состояния в деформированное, происходят так, что если вокруг какой-нибудь точки опишем шар весьма малого радиуса, то частицы, находившиеся в естественном состоянии внутри и на поверхности этого шара, в деформированном состоянии будут находиться внутри и на поверхности некоторого Э. Обратно, можно вокруг точки как вокруг центра описать такой Э., который при деформации обратится в шар; Э. этот называется Э. деформации.
Д. Б.
Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона. — С.-Пб.: Брокгауз-Ефрон. 1890—1907.
Синонимы:- Эллиот Эбенезер, поэт
- Эллис Александр, ученый
Смотреть что такое «Эллипсоид» в других словарях:
Эллипсоид — Эллипсоид. ЭЛЛИПСОИД, поверхность, которую можно получить из сферы, если сферу сжать (растянуть) в произвольных отношениях в трех взаимно перпендикулярных направлениях. Если эллипс вращать вокруг одной из его осей, то описываемая им поверхность… … Иллюстрированный энциклопедический словарь
ЭЛЛИПСОИД — (греч., от elleipsis эллипсис, и eidos сходство). Геометрическое тело, происходящее от обращения полуэллипса вокруг одной из своих осей. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ЭЛЛИПСОИД греч., от elleipsis … Словарь иностранных слов русского языка
Эллипсоид — вращения Эллипсоид поверхность в трёхмерном пространстве, полученная деформацией сферы вдоль трёх взаимно перпендикулярных осей. Каноническое уравнение эллипсоида в декартовых коор … Википедия
эллипсоид — а, м. ellipsoïde m. спец. Поверхность, образуемая вращением эллипса вокруг одной из своих осей. БАС 1. Глобусы в виде шара, груши, элипсоида. Кукольник Примеч. // К. 1851 1 556. Гало. Это эллипсоид диаметром более 600 тысяч световых лет,… … Исторический словарь галлицизмов русского языка
Эллипсоид — земной (a. earth ellipsoid; н. Erdellipsoid; ф. ellipsoide terrestre; и. elipsoide terrestre) эллипсоид вращения, наилучшим образом представляющий фигуру Геоида. Eго размеры и положение в теле Земли определяют из градусных измерений,… … Геологическая энциклопедия
эллипсоид — сущ., кол во синонимов: 5 • безгранник (2) • коноид (4) • референц эллипсоид (2) … Словарь синонимов
ЭЛЛИПСОИД — ЭЛЛИПСОИД, эллипсоида, муж. (мат.). Яйцевидное шарообразное тело, получающееся при вращении эллипса вокруг одной из своих осей. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
эллипсоид — а; м. [от греч. elleipsis выпадение, опущение и eidos вид] Матем. Поверхность, образуемая вращением эллипса (1.Э.; 1 зн.) вокруг одной из своих осей. ◁ Эллипсоидный, ая, ое. * * * эллипсоид замкнутая поверхность (2 го порядка). Эллипсоид можно… … Энциклопедический словарь
Эллипсоид — [ellipsoid] замкнутая центральная поверхность 2 го порядка. Эллипсоид имеет центр симметрии и три оси симметрии, которые называются осями эллипсоида: Смотри также: эллипсоид деформации эллипсоид напряжений … Энциклопедический словарь по металлургии
эллипсоид — 3.43 эллипсоид: Поверхность, полученная при вращении эллипсоида вокруг собственной оси. Примечание Параметры каждого эллипсоида определяются измерениями формы и размеров Земли, чтобы аппроксимировать геоид с наиболее возможно высокой точностью.… … Словарь-справочник терминов нормативно-технической документации
ЭЛЛИПСОИД — (от эллипс и греч. eidos вид) поверхность 2 го порядка. Может быть получена из поверхности шара, если шар сжать (растянуть) в произвольных отношениях в трёх взаимно перпендикулярных направлениях х, у, z (см. рис.). Если эллипс вращать вокруг… … Большой энциклопедический политехнический словарь
dic.academic.ru
Как правильно выбрать эллиптический тренажер для дома
В наше время сложно встретить современного молодого человека, который бы не занимался спортом. Мода на подтянутое стройное тело и здоровый образ жизни плотно поселилась в умах людей нашего тысячелетия. Но не у каждого и не всегда есть время на посещение спортивного зала. Выход из этой ситуации прост, купить тренажер для занятий дома и тренироваться в удобном для себя месте и в удобное время. Эллиптический тренажер или как его попросту называют в народе эллипс является бесспорным лидером в списке кардиотренажеров, используемых для похудения и сжигания лишних калорий. Давайте же попробуем разобраться как правильно выбрать эллиптический тренажер для занятий дома, на что нужно обращать внимание при выборе и какие бывают эти эллипсы.
Какой эллиптический тренажер выбрать для дома
Когда мы идем заниматься в спортивный зал, редко кто из нас задумывается какие тренажеры там стоят, более продвинутые пользователи могут обратить внимание на фирму спортивного инвентаря и его внешний вид, но редко кому в голову придет детально изучать характеристики тренажера, на пример, его габариты и вес, если конечно вы не являетесь хозяином этого зала или фитнес инструктором. Все гораздо сложнее, когда мы собираемся купить что-то для дома и покупка эллипса не исключение. Для начала необходимо определиться с моделью эллиптического тренажера.


Какие бывают эллиптические тренажеры
Производители предлагают на выбор потребителя три вида эллипсов: механические, магнитные и электромагнитные. Давайте попробуем разобраться, чем же они различаются.
Механические эллипсоиды
Механические эллипсоиды – самые компактные и легкие, что является несомненным их плюсом, поскольку мы говорим о покупке тренажера в квартиру. Среди своих конкурентов это самая простая и доступная модель.
Она приводится в движение от ремня, который натянут вокруг маховика. Регулировка нагрузки производится специальной ручкой. Тренажеры такой модели не зависят от источника питания. Среди минусов нужно отметить, что они являются, пожалуй, самыми шумными из всех представителей. К тому же такие тренажеры не могут похвастаться плавностью хода. Не смотря на привлекательную цену таких тренажеров нужно не забывать, что на таком эллипсе нельзя менять нагрузку, отслеживать состояние организма и количество потраченных калорий.
Магнитные эллипсы
Магнитные эллипсоиды – по своему устройству очень похожи на механические, но уже имеют возможность регулировать нагрузку. Движение в тренажерах такого вида происходит за счет магнитов, действующих на маховик.
В среднем, такие тренажеры имеют 8 уровней нагрузки. Эллиптические тренажеры такой модели оборудованы более совершенной системой торможения и гарантируют вам во время занятий тишину.
Электромагнитные эллипсоидные тренажеры
Электромагнитные устройства – самые современные и продвинутые эллиптические тренажеры, их обычно покупают для оборудования спортивных залов, но и в домашних условиях их использовать не запрещается. На сайте есть развернутая статья про электромагнитные эллиптические тренажеры.
Работают они от влияния электромагнитного поля на маховой элемент. Управление тренажером осуществляется с помощью встроенного компьютера. В таких тренажерах предусмотрены встроенные программы для разных типов тренировки, они снабжен датчиками движения и сердцебиения, которые оповещают если спортсмен перегружен. Эллиптические тренажеры такой модели оборудованы более совершенной системой торможения. Такие устройства работают от электросети и занимают много места.
Переднеприводные и заднеприводные эллипсоиды
В зависимости от места расположения маховика в эллиптическом тренажере они делятся на переднеприводные и заднеприводные, но какой же из них выбрать, давайте попробуем понять. Классикой эллипса считаются тренажеры с задним приводом, они появились раньше, чем переднеприводные. Основным их преимуществом, в первую очередь является цена, которая значительно меньше цены за покупку их переднеприводных братьев. И как не сложно понять из названия маховик и трансмиссия заднеприводных эллипсов расположены позади пользователя, что формирует траекторию движения при занятиях с углом наклона вперед, как при беге. Такие тренажеры обычно оборудованы длинной площадкой для ног, позволяющей менять положение тела в широких диапазонах. К тому же такие тренажеры достаточно компактны и занимают небольшое пространство при установке. Что же касается их качественных характеристик, то нужно отметить незначительный износ деталей и низкий уровень шума во время работы тренажера.
Переднеприводные эллиптические тренажеры, появились относительно не давно. Следуя логике понятно, что маховик и трансмиссия у них расположены в передней части тренажера, в результате чего тело тренирующегося человека фиксируется в вертикальном положении, без угла наклона. Эти модели подходят для людей любого роста, а особенно — для высоких спортсменов, потому что ручки, на такого вида тренажерах, расположены выше.


Чтобы все же понять какой тренажер выбрать именно вам передне или задне приводный стоит всего лишь попробовать их в действии, и вы сразу определитесь какой из видов эллипса вам подходит.
Подобрать эллиптический тренажер по параметрам
Теперь, когда мы разобрались в существующих моделях и разновидностях эллиптических тренажеров, давайте заглянем внутрь эллипса, в самое его сердце и узнаем из чего он состоит и как его составляющие могут повлиять на наш выбор при покупке тренажера.
Подбираем по длине шага
Длинной шага называют расстояние между начальной и конечной точкой движения педали. От нее зависит амплитуда движения ног, а, следовательно, ваше удобство и комфорт при тренировке на эллипсе. Это основной показатель эллипсоида, поэтому, мы выложили отдельную статью про длину шага на эллипсе, рекомендуем.
Как выяснилось оптимальной является длина шага, равная 40 сантиметров, ведь именно широкий шаг позволяет тренировать большее количество мышц, к тому же, чем выше пользователь, тем сильнее он ограничен в движениях при неправильном выборе длины.


Занятия на эллиптическом тренажер это по сути имитация ходьбы на лыжах, соответственно, чем шире размах ног во время тренировки, тем больше задействовано мышц. Чтобы выяснить свою длину шага нужно примерить тренажер и, если шаг будет достаточно длинный во время тренировок вы сможете полностью вытягивать ноги и чувствовать себя комфортно во время занятий на эллипсе. Если же длина шага будет ниже указанной отметки в 40 сантиметров, во время занятий выбудете чувствовать себя скованно и ограниченно в свободе выполнения движений.
Подбор эллиптического тренажера по росту
Признавайтесь есть среди читающих эту статью «Дяди степы», если ответ положительный, то эта информация для вас. Перечитайте еще раз внимательно предыдущий раздел о длине шага, для вас он особенно актуален, потому что для людей, чей рост начинается от 185 сантиметров и выше, рекомендуемая длина шага составляет от 50 сантиметров, в случае если вы остановили свой выбор в пользу переднеприводного тренажера и от 48 сантиметров – для заднеприводных моделей. Людям низкого и среднего роста – до 175 см – подойдут варианты с длиной шага от 40 сантиметров.
Эллиптический тренажер по весу пользователя
Выбор моделей эллиптических тренажеров для людей с весом тела выше среднего ограничен. Впрочем, из-за этого не стоит расстраиваться, это лишь упростит ваши муки выбора.
В инструкциях к некоторым тренажерам указывается максимальный рекомендуемый вес пользователя, в каких — то инструкциях встречается даже два показателя: рекомендуемый и максимально допустимый вес. Выбирая тренажер необходимо знать, что ваш вес должен быть меньше указанного максимального значения, по крайней мере 15 кг запаса необходимо оставить. Покупая, тренажер мы конечно рассчитываем максимально снизить наш вес, но пока это не произойдет, нам придется заниматься на тренажере, а не исполнение указаний инструкции производителя может привести к поломкам тренажера.
Вес маховика в эллиптическом тренажере
Одним из самых значимых при выборе эллиптического тренажера критериев является вес маховика. При помощи этой не хитрой штуковины определяется много функциональных возможностей тренажера: это и комфортность занятий на нем и качество самого тренажера и плавность вращения педалей.


Так смотря на характеристики маховика в устройстве эллиптического тренажера необходимо знать, что при весе в 7-10 килограмм маховик будет считаться легким, что будет ощущаться при вращении педалей тренажера, они будут отзываться неприятными рывками. Поэтому при выборе эллиптического тренажера эксперты советуют выбирать модели с маховиком, вес которого составляет не менее 11 килограмм. Более тяжелое колесо обеспечивает во время занятий плавность вращений и комфорт для занимающегося на тренажере.
Габариты эллипса
Приобретая эллиптический тренажер для занятий дома возникает резонный вопрос сколько места, он займет и где его расположить в квартире. Разные производители предлагают потребителю эллиптические тренажеры различных форм и размеров. Компактные или складные модели подойдут тем, кто ограничен в пространстве. Если помещение позволяет, то стоит обратить внимание на более продвинутые и большие по размеру модели. Знающие люди утверждают, что хороший эллипс должен быть большим и тяжелым, с помощью этих показателей достигается комфорт во время тренировок.
Эллипсоид: вес тренажера
Эллиптические тренажеры, предназначенные для занятий дома имеют меньший вес, легко перемещаются, могут складываться. Важно понимать, что чем массивней тренажер, тем он более устойчив. Важно при выборе тренажера обратить внимание на соотношение веса эллипса и максимальный вес пользователя. Так, на пример, эллиптический тренажер весом до 40 килограмм не сможет выдержать тренирующегося, весом в 140 килограмм.
Наклон педалей
Не мало важное значение при тренировке на эллипсе имеет угол наклона педалей тренажера. Поэтому выбирая какой эллиптический тренажер выбрать необходимо обратить внимание на тренажеры, в которых можно регулировать указанный показатель. Смена положения тела при тренировке на эллипсе важна для равномерной проработки различных групп мышц. Качественно проработать мышцы нижних конечност
elipsoid.ru
ЭЛЛИПСОИД — это… Что такое ЭЛЛИПСОИД?
Эллипсоид — Эллипсоид. ЭЛЛИПСОИД, поверхность, которую можно получить из сферы, если сферу сжать (растянуть) в произвольных отношениях в трех взаимно перпендикулярных направлениях. Если эллипс вращать вокруг одной из его осей, то описываемая им поверхность… … Иллюстрированный энциклопедический словарь
ЭЛЛИПСОИД — (греч., от elleipsis эллипсис, и eidos сходство). Геометрическое тело, происходящее от обращения полуэллипса вокруг одной из своих осей. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ЭЛЛИПСОИД греч., от elleipsis … Словарь иностранных слов русского языка
Эллипсоид — вращения Эллипсоид поверхность в трёхмерном пространстве, полученная деформацией сферы вдоль трёх взаимно перпендикулярных осей. Каноническое уравнение эллипсоида в декартовых коор … Википедия
эллипсоид — а, м. ellipsoïde m. спец. Поверхность, образуемая вращением эллипса вокруг одной из своих осей. БАС 1. Глобусы в виде шара, груши, элипсоида. Кукольник Примеч. // К. 1851 1 556. Гало. Это эллипсоид диаметром более 600 тысяч световых лет,… … Исторический словарь галлицизмов русского языка
Эллипсоид — земной (a. earth ellipsoid; н. Erdellipsoid; ф. ellipsoide terrestre; и. elipsoide terrestre) эллипсоид вращения, наилучшим образом представляющий фигуру Геоида. Eго размеры и положение в теле Земли определяют из градусных измерений,… … Геологическая энциклопедия
эллипсоид — сущ., кол во синонимов: 5 • безгранник (2) • коноид (4) • референц эллипсоид (2) … Словарь синонимов
ЭЛЛИПСОИД — ЭЛЛИПСОИД, эллипсоида, муж. (мат.). Яйцевидное шарообразное тело, получающееся при вращении эллипса вокруг одной из своих осей. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
эллипсоид — а; м. [от греч. elleipsis выпадение, опущение и eidos вид] Матем. Поверхность, образуемая вращением эллипса (1.Э.; 1 зн.) вокруг одной из своих осей. ◁ Эллипсоидный, ая, ое. * * * эллипсоид замкнутая поверхность (2 го порядка). Эллипсоид можно… … Энциклопедический словарь
Эллипсоид — [ellipsoid] замкнутая центральная поверхность 2 го порядка. Эллипсоид имеет центр симметрии и три оси симметрии, которые называются осями эллипсоида: Смотри также: эллипсоид деформации эллипсоид напряжений … Энциклопедический словарь по металлургии
эллипсоид — 3.43 эллипсоид: Поверхность, полученная при вращении эллипсоида вокруг собственной оси. Примечание Параметры каждого эллипсоида определяются измерениями формы и размеров Земли, чтобы аппроксимировать геоид с наиболее возможно высокой точностью.… … Словарь-справочник терминов нормативно-технической документации
ЭЛЛИПСОИД — (от эллипс и греч. eidos вид) поверхность 2 го порядка. Может быть получена из поверхности шара, если шар сжать (растянуть) в произвольных отношениях в трёх взаимно перпендикулярных направлениях х, у, z (см. рис.). Если эллипс вращать вокруг… … Большой энциклопедический политехнический словарь
dic.academic.ru
эллипсоид — это… Что такое эллипсоид?
Эллипсоид — Эллипсоид. ЭЛЛИПСОИД, поверхность, которую можно получить из сферы, если сферу сжать (растянуть) в произвольных отношениях в трех взаимно перпендикулярных направлениях. Если эллипс вращать вокруг одной из его осей, то описываемая им поверхность… … Иллюстрированный энциклопедический словарь
ЭЛЛИПСОИД — (греч., от elleipsis эллипсис, и eidos сходство). Геометрическое тело, происходящее от обращения полуэллипса вокруг одной из своих осей. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ЭЛЛИПСОИД греч., от elleipsis … Словарь иностранных слов русского языка
Эллипсоид — вращения Эллипсоид поверхность в трёхмерном пространстве, полученная деформацией сферы вдоль трёх взаимно перпендикулярных осей. Каноническое уравнение эллипсоида в декартовых коор … Википедия
эллипсоид — а, м. ellipsoïde m. спец. Поверхность, образуемая вращением эллипса вокруг одной из своих осей. БАС 1. Глобусы в виде шара, груши, элипсоида. Кукольник Примеч. // К. 1851 1 556. Гало. Это эллипсоид диаметром более 600 тысяч световых лет,… … Исторический словарь галлицизмов русского языка
Эллипсоид — земной (a. earth ellipsoid; н. Erdellipsoid; ф. ellipsoide terrestre; и. elipsoide terrestre) эллипсоид вращения, наилучшим образом представляющий фигуру Геоида. Eго размеры и положение в теле Земли определяют из градусных измерений,… … Геологическая энциклопедия
эллипсоид — сущ., кол во синонимов: 5 • безгранник (2) • коноид (4) • референц эллипсоид (2) … Словарь синонимов
ЭЛЛИПСОИД — ЭЛЛИПСОИД, эллипсоида, муж. (мат.). Яйцевидное шарообразное тело, получающееся при вращении эллипса вокруг одной из своих осей. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
Эллипсоид — [ellipsoid] замкнутая центральная поверхность 2 го порядка. Эллипсоид имеет центр симметрии и три оси симметрии, которые называются осями эллипсоида: Смотри также: эллипсоид деформации эллипсоид напряжений … Энциклопедический словарь по металлургии
эллипсоид — 3.43 эллипсоид: Поверхность, полученная при вращении эллипсоида вокруг собственной оси. Примечание Параметры каждого эллипсоида определяются измерениями формы и размеров Земли, чтобы аппроксимировать геоид с наиболее возможно высокой точностью.… … Словарь-справочник терминов нормативно-технической документации
ЭЛЛИПСОИД — (от эллипс и греч. eidos вид) поверхность 2 го порядка. Может быть получена из поверхности шара, если шар сжать (растянуть) в произвольных отношениях в трёх взаимно перпендикулярных направлениях х, у, z (см. рис.). Если эллипс вращать вокруг… … Большой энциклопедический политехнический словарь
dic.academic.ru


